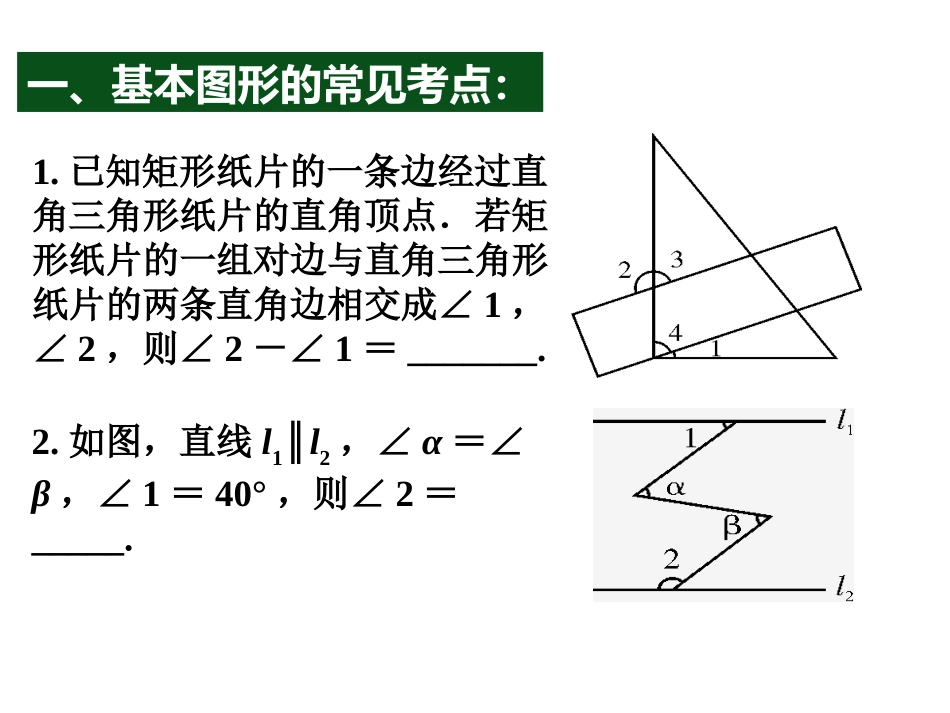
中考复习四:图形的认识点、相交线、三角形、四边形1.点与距离2.角平分线与中垂线3.三角形:三线合一与三心4.四边形:性质与判定5.多边形:内角和与外角和一、基本图形的常见考点:1.已知矩形纸片的一条边经过直角三角形纸片的直角顶点.若矩形纸片的一组对边与直角三角形纸片的两条直角边相交成∠1,∠2,则∠2-∠1=_______.2.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=_____.一、基本图形的常见考点:3.如图,∠AOB为直角,OM平分∠BOC,ON平分∠AOC.若∠AOC=50°,则∠MON的度数=_________.4、(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,线段MN的长度=___________;(2)在(1)中,如果AC=acm,BC=bcm,其他条件不变,线段MN的长度=___________.二、三角形常见考点:1.如图1,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的()A.AB=CD;B.EC=BF;C.∠A=∠D;D.AB=BC2.如图2,在△ABC中,若∠1=∠2,BE=CD,AB=5,AE=2,则CE=________.3.如图3,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是()A.1对B.2对C.3对D.4对二、三角形常见考点:4.(2015年四川南充)如图4,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是________.5.如图4316,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为________.6.如图5,在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为________.二、三角形常见考点:二、三角形常见考点:7.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADC的面积为S1,△ACE的面积为S2.若SABC△=6,则S1-S2的值为______.8.如图,在RtABC△中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=________.1.(2015年四川广元)一个多边形的内角和是外角和的2倍,这个多边形的边数为()A.5B.6C.7D.82.一个多边形的每个内角均为120°,这个多边形是()A.四边形B.五边形C.六边形D.七边形三、多边形常见考点:3.如图3,在矩形ABCD中,AB=10,BC=5,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则阴影部分图形的周长为()A.15B.20C.25D.304.如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是________三、多边形常见考点:三、多边形常见考点:5.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于_______.6.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C坐标为_____.三、多边形常见考点:7.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.(1)从运动开始,当t取何值时,PQ∥CD?(2)从运动开始,当t取何值时,△PQC为直角三角形?8.如图(1),在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图(2),把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.三、多边形常见考点:中考典型题1.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形.下列结论中:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④CD·AE=EF·CG;一定正确的结论有()A.1个B2个C3个D.4个BACDFEG∟∟2.梯形ABCD中,ADBC∥,对角线ACBD,AB=DC,⊥且AD=3,BC=5,则梯形面积=________.中考典型题ABCD∟∟3.(1)证明三角形中位线定理:三角形的中位线平行于第三边...