三角函数模型的简单应用VIP免费

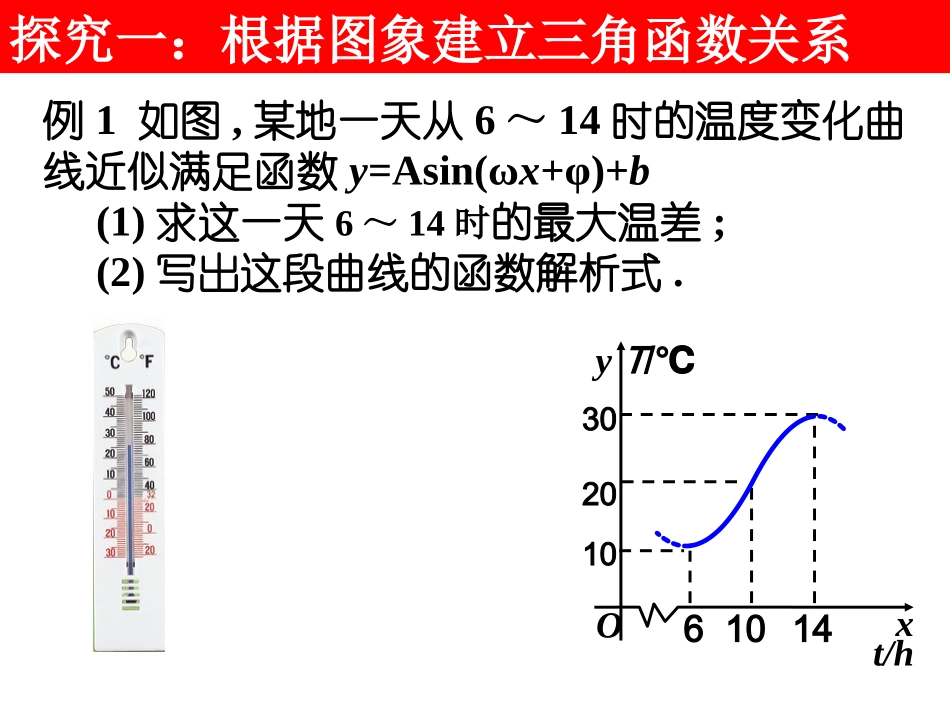
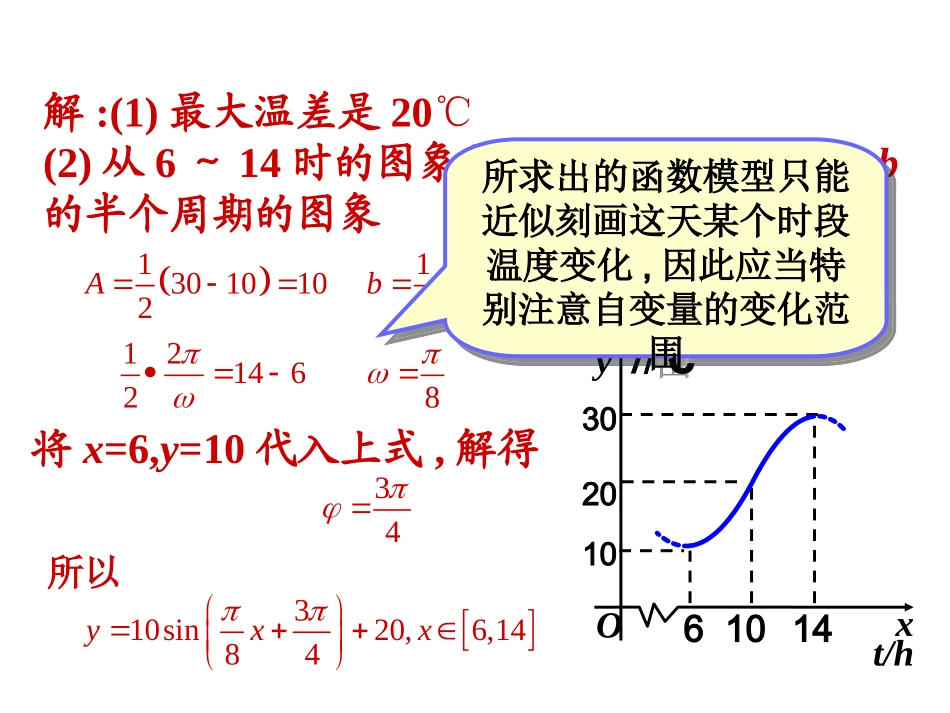
1.6三角函数模型的简单应用例1如图,某地一天从6～14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(1)求这一天6～14时的最大温差;(2)写出这段曲线的函数解析式.61014yT/℃xt/h102030O探究一：根据图象建立三角函数关系解:(1)最大温差是20℃(2)从6～14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象61014yT/℃xt/h102030O13010102A13010202b1214628将x=6,y=10代入上式,解得34310sin20,6,1484yxx所求出的函数模型只能近似刻画这天某个时段温度变化,因此应当特别注意自变量的变化范围所求出的函数模型只能近似刻画这天某个时段温度变化,因此应当特别注意自变量的变化范围所以题型总结：maxmin1A=fx-fx2maxmin1b=fx+fx2利用求得2πT=，ωω利用最低点或最高点在图象上该点的坐标满足函数解析式可求得,φ也可以利用函数的零值点来求．f求函数的方法：(x)=Asin(x+)+b例2画出函数y=|sinx|的图象并观察其周期.xy-11O2222y=|sinx|解周期为π验证:|sin(x+π)|=|-sinx|=|sinx|利用函数图象的直观性，通过观察图象而获得对函数性质的认识，这是研究数学问题的常用方法。显然，函数y=|sinx|与正弦函数有紧密的联系，你能利用这种联系说说它的图象的作法吗？正弦函数y=sinx的图象保留x轴上方部分，将x轴下方部分翻折到x轴上方，得到y=|sinx|的图象δφθφ-δ太阳光例3如图,设地球表面某地正午太阳高度角为θ,δ为此时太阳直射纬度,φ为该地的纬度值,那么这三个量之间的关系是θ=90°-|φ-δ|.当地夏半年δ取正值,冬半年δ负值.如果在北京地区(纬度数约为北纬40°)的一幢高为h0的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?课件演示探究二：建立三角函数模型求临界值分析：太阳高度角、楼高h0与此时楼房在地面的投影长h之间的有如下关系：h0=htan23262326040MhCBA根据地理知识，在北京地区，太阳直身北回归线时物体的影子最短，直射南回归线时物体的影子最长.考虑太阳直射南回归线解:取太阳直射南回归线的情况考虑,此时太阳直射纬度为-23°26′,依题意两楼的间距应不小于MC.根据太阳高度角的定义,有,432662234090C000000.24326tantanhhChMC所以即在盖楼时,为使后楼不被前楼遮挡,要留出相当于楼高两倍的间距例4海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:时刻水深/米时刻水深/米时刻水深/米0:005.09:002.518:005.03:007.512:005.021:002.56:005.015:007.524:005.0探究三：根据相关数据进行三角函数拟合(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值(精确到0.001).(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?(3)若某船的吃水深度为4米.安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?课件演示解:(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图3691215182124Oxy642根据图象,可以考虑用函数y=Asin(x+)+h刻画水深与题意之间的对应关系.A=2.5,h=5,T=12,=0.612,2T得由所以,港口的水深与时间的关系可用近似描述.56sin5.2xy时刻0:001:002:003:004:005:006:007:008:009:0010:0011:00水深5.0006.2507.1657.57.1656.2505.0003.7542.8352.5002.8353.754时刻12:0013:0014:0015:0016:0017:0018:0019:0020:0021:0022:0023:00水深5.0006.2507.1657.57.1656.2505.0003.7542.8352.5002.8353.75456sin5.2xy由得到港口在整点时水深的近似值:(2)货船需要的安全水深为4+1.5=5.5(米),所以当y≥5.5时就可以进港.5.556sin5.2x2.06sinx由计算器可得SHIFTs...