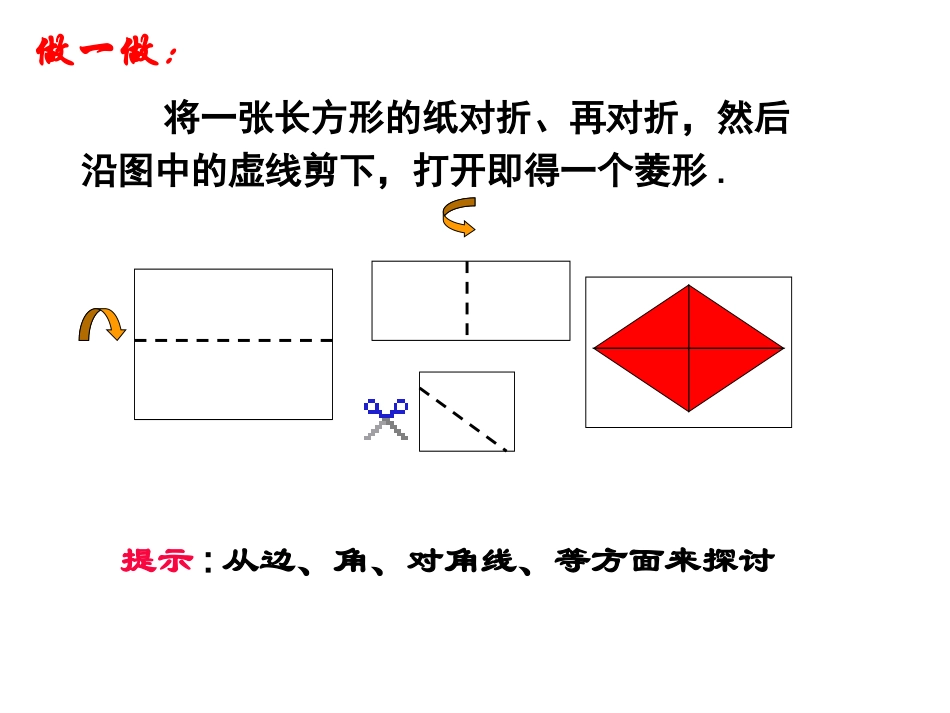
菱形的性质授课者:阮群愉一组邻边相等有一组邻边相等的平行四边形叫做菱形平行四边形菱形AB=BCABCD四边形ABCD是菱形做一做:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即得一个菱形.提示:从边、角、对角线、等方面来探讨BDAC菱形既是轴对称图形又是中心对称图形。做一做:通过上面的折纸活动,可以发现:因为菱形是特殊的平行四边形,所以具有平行四边形的所有性质。菱形的四条边都相等;菱形的对角线互相垂直;菱形的每一条对角线平分一组对角。证明:菱形的四条边都相等;菱形的对角线互相垂直;菱形的每一条对角线平分一组对角。已知:如图,在菱形ABCD中,AB=BC,对角线AC与BD相交于点O.求证:(1)AB=BC=CD=ADADCBOADCBO∵四边形ABCD是菱形∴AB=BC=CD=DA即ACBD⊥∴AC平分∠BAD和∠BCD又∵AC=AC∴△ADC≌ABC△∵四边形ABCD是菱形∴AB=AD,OD=OB∴在等腰三角形ABD中AOBD⊥证明:(2)AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC(3)AC⊥BD同理:BD平分∠ABC和∠ADC菱形的两条对角线互相平分菱形的两组对边平行且相等边对角线角菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直,且每一条对角线平分一组对角。ADCBO相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BCOA=OCOB=OD∠DAB=BCDABC=CDA∠∠∠∠AOB=DOC=AOD=BOC=90°∠∠∠∠1=2=3=45=6=7=8∠∠∠∠∠∠∠△ABCDBCACDABD△△△RtAOBRtBOCRtCOD△△△RtDOA△RtAOBRtBOCRtCODRtDOA△≌△≌△≌△△ABDBCDABCACD≌△△≌△ABCDO123456781.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.ODCBA3cm60度3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是()CA.10cmB.7cmC.5cmD.4cmABCDO344.在菱形ABCD中,AEBC⊥,AFCD⊥,E、F分别为BC,CD的中点,那么∠EAF的度数是()FECABDA.75°B.60°C.45°D.30°B5、四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。ABCDO94522222OAABOB解:∵四边形ABCD是菱形∴ACBD⊥∴∴OB=3∴BD=2OB=6cm543有关菱形问题可转化为直角三角形或等腰三角形的问题来解决例1:如图,菱形ABCD的边长为4cm,∠BAD=1200。对角线AC、BD相交于点O,求这个菱形的对角线长。ODCBA解:∵∠BAD=1200∴∠BAC=600又∵AB=BC∴△BAC是等边三角形∴AC=4cm∴BO=2√3∴BD=4√3补充例题:已知如图,菱形ABCD中,E是AB的中点,且DEAB⊥,AB=1。求(1)∠ABC的度数;(2)对角线AC、BD的长;ABCDEOABCDEO2∵四边形ABCD是菱形,∴AD=AB解:∴AD=AB=BD∵E是AB的中点,且DEAB⊥∴DA=DB(DE为AB的中垂线)∴∠DAB=60°,∴∠ABC=120°(2)∵AE=2,∴AB=4BD=AB=4∴∵四边形ABCD是菱形,∴ACDB⊥∵DB=40B=2∴∴在Rt△AOB中,由勾股定理得242222BOAB23AO=∴AC=43(3)在Rt△DAE中,由勾股定理得DE=242222AEAD=23(1)填空题1.菱形的一个内角为120°,平分这个内角的对角线长为11厘米,菱形的周长为______.2.菱形的对角线的一半的长分别为8cm和11cm,则菱形的面积是_______.3.菱形的面积为64平方厘米,两条对角线的比为12∶,那么菱形的边长为_______.4.已知,菱形对角线长分别为12cm和16cm,求菱形的高。44厘米176cm28厘米5.菱形具有而一般平行四边形不具有的性质是()A.对角相等B.对边相等C.对角线互相垂直D.对角线相等6.如图,在边长为6的菱形ABCD中,∠DAB=60º,E是AB的中点,F是AC上的动点,则EF+BF的最小值为AEFDCB