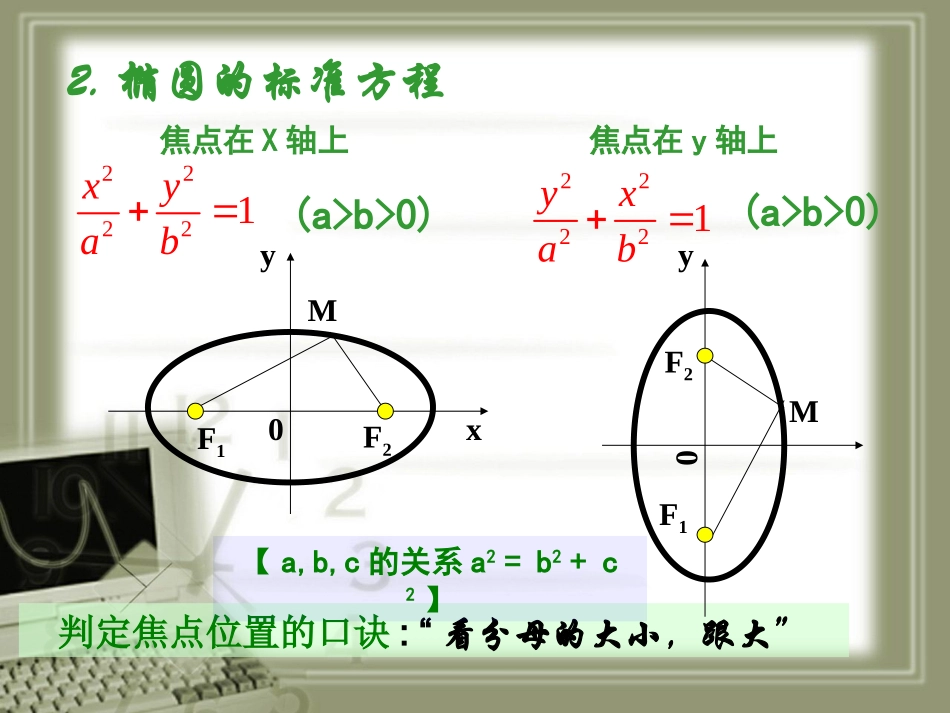
温故1.椭圆的定义平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫作椭圆。数学表达式为|PF1|+|PF2|=2a(2a>2c)这两个定点叫做椭圆的焦点。两焦点间的距离叫做椭圆的焦距.2.椭圆的标准方程焦点在X轴上焦点在y轴上(a>b>0)22221xyab(a>b>0)22221yxab判定焦点位置的口诀:“看分母的大小,跟大”F1F2M0xyF1F2M0y【a,b,c的关系a2=b2+c2】知新一、椭圆的范围oxy由11122222222byaxbyax且即说明:椭圆位于直线X=±a和y=±b所围成的矩形之中。如右图二、椭圆的对称性)0(12222babyax在之中,把()换成(),方程不变,说明:椭圆关于()轴对称;椭圆关于()轴对称;椭圆关于()点对称;故:坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心oxy三、椭圆的顶点)0(12222babyax在中,令x=0,得y=?,说明椭圆与y轴的交点是()令y=0,得x=?说明椭圆与x轴的交点是()*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。切记:焦点总在长轴上!a、b分别叫做椭圆的长半轴长和短半轴长。oxyB1(0,b)B2(0,-b)A1A2四、椭圆的离心率oxyace离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:因为a>c>0,所以1>e>0[2]离心率对椭圆形状的影响:1)e越接近1,c就越接近a,从而b就越小(?),椭圆就越扁(为啥?)2)e越接近0,c就越接近0,从而b就越大(?),椭圆就越圆(为啥?)3)特例:e=0,则a=b,则c=0,两个焦点重合,椭圆方程变为(为啥?)_归纳vs迁移标准方程图象范围对称性顶点坐标焦点坐标半轴长焦距a,b,c关系离心率22221(0)xyabab22221(0)xyabba|x|≤a,|y|≤b|x|≤b,|y|≤a关于x轴、y轴成轴对称;关于原点成中心对称。(a,0),(0,b)(b,0),(0,a)(c,0)(0,c)长半轴长为a,短半轴长为b.焦距为2c;a2=b2+c2cea例1已知椭圆方程为16x2+25y2=400,它的长轴长是:。短轴长是:。焦距是:。离心率等于:。焦点坐标是:。顶点坐标是:。外切矩形的面积等于:。108635(3,0)(5,0)(0,4)80已知椭圆方程为6x2+y2=6它的长轴长是:。短轴长是:。焦距是:。离心率等于:。焦点坐标是:。顶点坐标是:。外切矩形的面积等于:。可以为师矣例2.已知椭圆中心在原点,对称轴为坐标轴,一个焦点在y,长轴是短轴的2倍,焦距为2,离心率为/2,且过(2,-6)求椭圆的方程。求椭圆的标准方程时,应:先定型(焦点),再定量(a、b)当焦点位置不确定时,要讨论,此时有两个解!小结:基本元素oxyB1(0,b)B2(0,-b)A1A21)基本量:a、b、c、e、(共四个量)2)基本点:顶点、焦点、中心(共七个点)3)基本线:对称轴、(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)作业:课本第68页习题第2、3、7题实践出能力下课啦!谢谢指导!