分式的加法和减法VIP免费

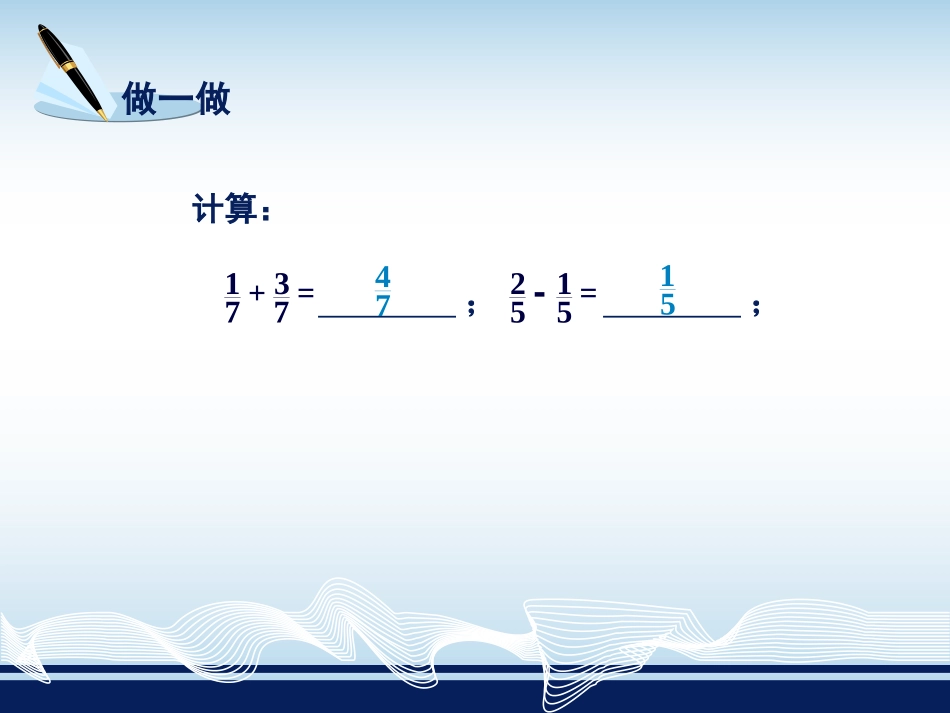
分式的加法和减法本课内容本节内容1.4做一做13+=7721=55-；；计算：4715类似地，同分母的分式的加、减法运算法则是：同分母的分式相加减，分母不变，把分子相加减.=±±ffhh.ggg即同分母的分数相加减，分母不变，把分子相加减.41751332+==7755.；-例1计算：举例2331+2++()()yxyxxxyxyxyxy；.---1+++解()yxxyxy+=+xyxy233=xxyxy--.=3x=12332()xyxxyxy.---3=xxyxy--()分式运算的最后结果要化为最简分式.分式运算的最后结果要化为最简分式.注意下列等式是否成立？为什么？说一说==----ffffgggg，.0===0fff+f+gggg--()，因为所以=.ffgg--因为所以=--ffgg，=.--ffgg例2计算：举例+acbcabba--+acbcabba解--acbc=+abab---()acbc=abab---acbc=ab--cab=ab--()=c练习1.计算：7381+xxx-()；2x答案：222++yxxyxy-()；22223().acbcabab---答案：x-yca+b答案：2.计算：221+()；ababba--答案：a+b.233+3223().yxxyyx--答案：1+22+()；mnnnmmn--m+nnm答案：-做一做11+=2321=53-；.计算：325666651151515516151121+==5233；.-异分母的分数相加减，要先通分，化成同分母的分数，再加减.类似地，异分母的分式进行加、减运算时，也要先化成同分母的分式，然后再加减.根据分式的基本性质，把几个异分母的分式化成同分母的分式的过程，叫作分式的通分.动脑筋如何把分式通分？1123xy，通分时，关键是确定公分母.一般取各分母的所有因式的最高次幂的积作为公分母，这样的公分母称为最简公分母.通分时，关键是确定公分母.一般取各分母的所有因式的最高次幂的积作为公分母，这样的公分母称为最简公分母.2x的因式有2，x；两式中所有因式的最高次幂的积是6xy，1123xy，3y的因式有3，y，所以这两个分式的最简公分母为6xy.2x3y从而可以根据分式的基本性质，分别把原来各分式的分子和分母都乘同一个适当的整式，使各分式的分母都化成6xy.131==22633，yxxyxyy通分过程如下:112==33622.xyyxxyx举例例3通分：22221143y4352542xxyacbbcabac()，()，，.；21143yxxy()，222244==33412xxxxyyxxy··，解最简公分母是12xy2.21331==44312yyxyxyyxy··.2322222244416==55420aaacacbcbcacabc··，最简公分母是20a2b2c2.2322222233515==44520ccbcbcababbcabc··，2224352542acbbcabac()，，.23222222551050==221020bbababacacababc··.举例例4通分：2211112424()，()，.xxxxxx；---2111()，xxx-；11=1xxxx，()--解最简公分母是x(x-1).211=1xxxx.()--212=2+224xxx，--()()最简公分母是2(x+2)(x-2).+2==42222+22.()()()()xxxxxxxx-----212424()，.xxx--练习1.通分：11146xy(),；3112412612,yx==xxyyxy答案：32222224721824624yyx==xyxyxxy答案：,75278yx(),；223bcab(),；227486yxyx(),.497540785656答案：yx==yxxyxy,32222222答案：bbcac==aabbab,2.通分：2312+3+(),()()yxyxyxxy2239=2+6+24=3+6+,()().()()xxyxyxyxyyyxxyxyxy答案：212y.yxxxy--(),211==xxyxxyyxy.yxxxy,()()答案：-----动脑筋从甲地到乙地依次需经过1km的上坡路和2km的下坡路.已知小明骑车在上坡路上的速度为vkm/h，在下坡路上的速度为3vkm/h，则他骑车从甲地到乙地需多长时间？这是异分母的分式的加法，因此我们应先把它们化成同分母的分式，然后再相加，即小明骑车走1km上坡路和2km下坡路的时间分别为，，那么骑行所需的总时间为.1hv2h3v12+h3vv12+332=+333+25==.33vvvvvv因此，小明骑车从甲地到乙地需.5h3v举例例5计算：1492234--yxxyabc+baab()().；149()yxxy-94=4994yyxxxyyx-解2294=36.yxxy-643=263443aabbc+baabab-2264+3=12.abcab-2234-abc+baab()举例例6计算：222161++391321-----xxxxx+xx()().；2161++39-xx()16=++3+33xxx-()()解36=++33+33xxxxx---()()()()+3=+33xxx-()()1=.3x-13=111xxxx+x+x----()()()221321()xxx+xx----213=1111xxxxx+xxx+x-----()()()()()()22213=11xx+xxxx+x----()()()1=11x+xx+x-()()1=.1xx-()举例例3计算：1+1+1xx-.1+1+1xx解-+11=+11xx-+111=+11()()xxxx---1+1+1=1()()xxx--21+1=1xx--22=1--xx注意把“x+1”看作“”，有助于寻找两个分式的公分母.+11x练习1.计算：...