简单的线性规划问题BVIP免费

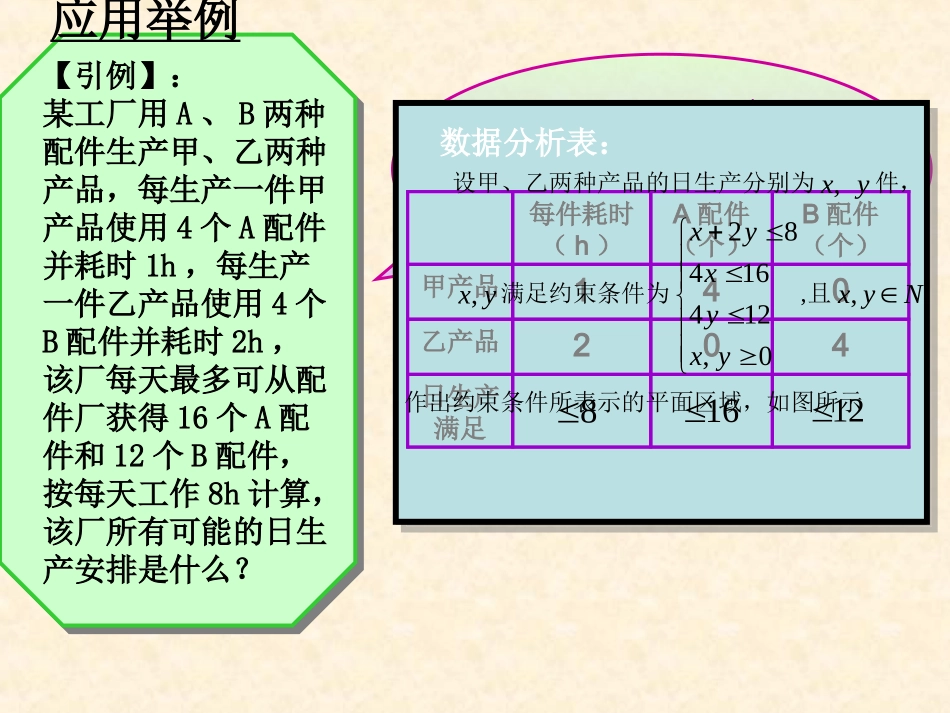
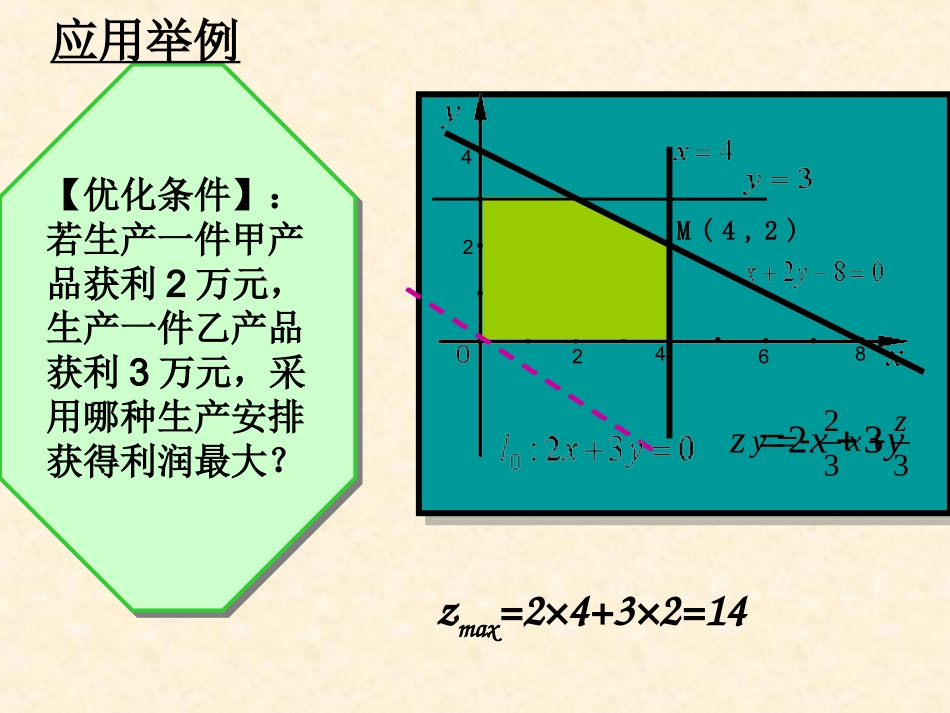
第三章不等式3.3.2简单的线性规划问题符洪峰如果若干年后的你成为某工厂的厂长，你将会面对生产安排、资源利用、人力调配的问题……【引例】：某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件并耗时1h，每生产一件乙产品使用4个B配件并耗时2h，该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天工作8h计算，该厂所有可能的日生产安排是什么？数据分析表：日生产满足402乙产品041甲产品B配件（个）A配件（个）每件耗时（h）12816设甲、乙两种产品的日生产分别为,xy件，,xy满足约束条件为28416412,0xyxyxy,且,xyN作出约束条件所表示的平面区域，如图所示应用举例248642【优化条件】：若生产一件甲产品获利2万元，生产一件乙产品获利3万元，采用哪种生产安排获得利润最大？M(4,2)233zyx23zxy应用举例zmax=2×4+3×2=14线性规划：求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题•可行解：满足线性约束条件的解(x，y)叫可行解；•可行域：由所有可行解组成的集合叫做可行域；•最优解：使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。解线性规划问题的步骤：2、在线性目标函数所表示的一组平行线中，用平移的方法找出与可行域有公共点且纵截距最大或最小的直线；（注意y的系数“+，-”）3、通过解方程组求出最优解；4、作出答案。1、画出线性约束条件所表示的可行域；画移求答•解线性规划应用问题的一般步骤：•1、理清题意，列出表格；•2、设好变元，列出线性约束条件（不等式组）与目标函数；•3、准确作图；•4、根据题设精确度计算。例1营养学家指出，成人良好的日常饮食应该至少提供0.075kg的碳水化合物，0.06kg的蛋白质，0.06kg的脂肪，1kg食物A含有0.105kg碳水化合物，0.07kg蛋白质，0.14kg脂肪，花费28元；而1食物B含有0.105kg碳水化合物，0.14kg蛋白质，0.07kg脂肪，花费21元。为了满足营养专家指出的日常饮食要求，同时使花费最低，需要同时食用食物A和食物B多少kg？食物／kg碳水化合物／kg蛋白质/kg脂肪／kgAB分析：将已知数据列成表格0.1050.1050.070.140.140.07日常饮食含量0.0750.060.06解：设每天食用xkg食物A，ykg食物B，总成本为z，那么00671461475770006.007.014.006.014.007.0075.010.0105.0yxyxyxyxyxyxyxyx＋＋目标函数为：z＝28x＋21y作出二元一次不等式组所表示的平面区域，即可行域把目标函数z＝28x＋21y变形为xyo5/75/76/73/73/76/72834zxy它表示斜率为随z变化的一组平行直线系34是直线在y轴上的截距，当截距最小时，z的值最小。28zM如图可见，当直线z＝28x＋21y经过可行域上的点M时，截距最小，即z最小。M点是两条直线的交点，解方程组6714577yxyx得M点的坐标为：7471yx所以zmin＝28x＋21y＝16由此可知，每天食用食物A143g，食物B约571g，能够满足日常饮食要求，又使花费最低，最低成本为16元。Àý2Òª½«Á½ÖÖ´óС²»Í¬µÄ¸Ö°å½Ø³ÉA¡¢B¡¢CÈýÖÖ¹æ¸ñ£¬Ã¿ÕŸְå¿Éͬʱ½ØµÃÈýÖÖ¹æ¸ñµÄС¸Ö°åµÄ¿éÊýÈçϱíËùʾ£A¹æ¸ñB¹æ¸ñC¹æ¸ñµÚÒ»ÖÖ¸Ö°å211µÚ¶þÖÖ¸Ö°å123½ñÐèÒªA¡¢B¡¢CÈýÖÖ¹æ¸ñµÄ³ÉÆ··Ö±ðΪ15¡¢18¡¢27¿é£¬Îʸ÷½ØÕâÁ½ÖÖ¸Ö°å¶àÉÙÕſɵÃËùÐèÈýÖÖ¹æ¸ñ³ÉÆ·£¬ÇÒʹËùÓøְåÕÅÊý×îÉÙ.解：设需截第一种钢板x张，第二种钢板y张2x+y15x+2y18x+3y27x0y0约束条件是作出可行域见课本图3.3-12目标函数是z=x+y此问题中，钢板张数为整数，在一组平行直线x+y=t中（t为参数），经过的整点是B(3,9)和C(4,8),它们是最优解518虽然直线经过点A时，与原点距离最近，539经过可行域内的整点（横坐标和纵坐标都是整数的点）且与原点距离最近的直线是x+y=12,但是由得273152yxyx...