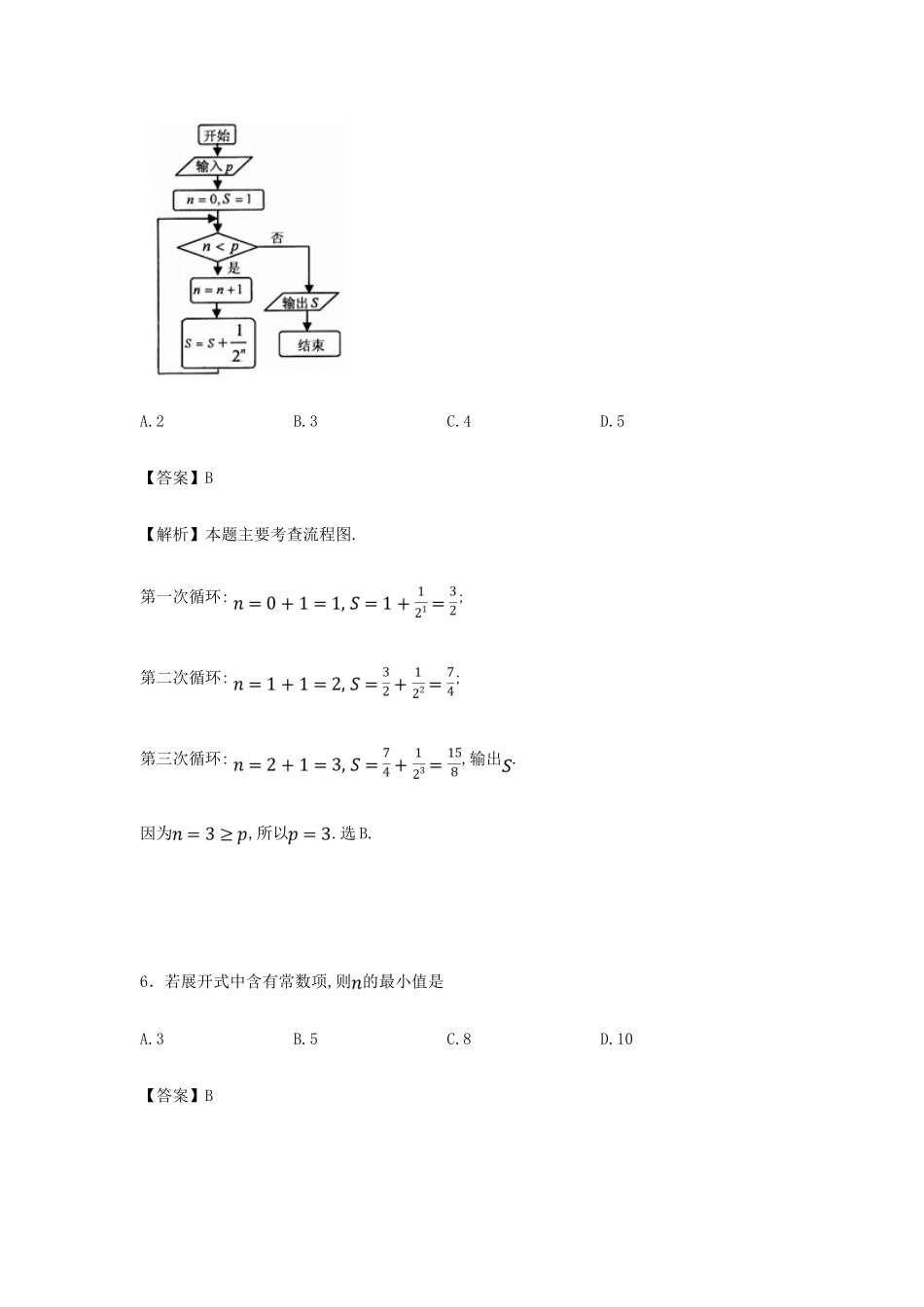
吉林省东北师范大学附属中学2016届高三第六次模拟考试数学一、选择题:共12题1.已知集合,则A.B.C.D.【答案】B【解析】本题主要考查集合的基本运算,对数函数.,所以.选B.【备注】集合的基本运算为高考常考题型,要求熟练掌握.2.已知复数为纯虚数,那么实数A.B.C.D.【答案】C【解析】本题主要考查复数的概念与运算.由题意知,,因为复数为纯虚数,所以且,所以.选C.3.已知命题:“”,命题:“直线与直线互相垂直”,则命题是命题的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】本题主要考查充分不必要条件,两直线的位置关系.当时,直线与直线互相垂直;当直线与直线互相垂直时,或.所以命题是命题的充分不必要条件.选A.4.我国古代数学名著《数书九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1536石,验得米内夹谷,抽样取米一把,数得224粒内夹谷28粒,则这批米内夹谷约A.134石B.169石C.192石D.338石【答案】C【解析】本题主要考查简单随机抽样.设这批米内夹谷约石,由题意得:,解得,.选C.5.执行如图所示的程序框图,若输出,则输入的值为A.2B.3C.4D.5【答案】B【解析】本题主要考查流程图.第一次循环:;第二次循环:;第三次循环:,输出.因为,所以.选B.6.若展开式中含有常数项,则的最小值是A.3B.5C.8D.10【答案】B【解析】本题主要考查二项式定理.由题意得=,而成立,所以,所以的最小值是5.选B.【备注】二项展开式的通项公式:.7.一个多面体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该多面体的表面积为A.2B.C.D.【答案】D【解析】本题主要考查三视图,空间几何体的表面积.该多面体为横放的三棱柱(如图所示);所以其表面积.选D.8.已知是与的等比中项,若则有A.最小值10B.最小值C.最大值10D.最大值【答案】B【解析】本题主要考查等比中项和对数的运算,基本不等式.因为是与的等比中项,所以;而,所以,所以,即,所以(当且仅当时等号成立);所以有最小值.选B.【备注】用均值不等式时,注意等号成立的条件.9.在Δ中,为线段的三等分点,则=A.B.C.D.【答案】C【解析】本题主要考查平面向量的数量积.因为,所以;因为为线段的三等分点,所以,所以=()==.选C.10.已知点是双曲线的一个焦点,过点且斜率为的直线与圆相切,则双曲线的离心率为A.B.C.2D.3【答案】C【解析】本题主要考查直线与圆的位置关系,双曲线的几何性质.令,则直线,即;而直线与圆相切,所以,可得双曲线的离心率.选C.【备注】双曲线,离心率.11.如图,棱长为1的正方体中,为线段上的动点,则下列结论正确的有①三棱锥的体积为定值②③的最大值为90°④的最小值为2A.①②B.①②③C.③④D.②③④【答案】A【解析】本题主要考查空间几何体的体积,线面平行与垂直,余弦定理.因为平面,所以三棱锥底面上的高为定值1,所以三棱锥的体积为定值,①正确;因为,所以平面;而在平面内,所以,②正确;当时,为钝角,③错误;将面与面展开(如图所示),此时为的最小值,在三角形中,由余弦定理得,即的最小值为.即④错误;所以结论正确的有①②.选A.【备注】体会数形结合思想.12.已知曲线上一点,曲线上一点,当时,对于任意,都有恒成立,则的最小值为A.1B.C.D.【答案】C【解析】本题主要考查导数在研究函数中的应用.由题意得,而,由图可得;所以;所以恒成立;构造函数),而,可得;当单减,当单增;所以;所以,即,即的最小值为.【备注】体会数形结合思想,化归与转化思想.二、填空题:共4题13.已知实数满足约束条件,则的最大值为.【答案】6【解析】本题主要考查线性规划问题.画出可行域(如图所示),;当过点时,取得最大值.14.已知抛物线,过焦点,且倾斜角为60°的直线与抛物线在第一象限交于点,若,则抛物线方程为.【答案】【解析】本题主要考查抛物线的标准方程.如图(画出图形),抛物线的焦点,准线;由题意得,即,即;而的倾斜角为60°,所以;将点代入可得或4;所以,即抛物线方程为.【备注】体会数形结合思想、化归与转化思想.15.将函数的图象向右平移个单位后得到函数的图象,则由函数与的图象所围成的封闭图形的面积为.【答案】2【解析】本题主要考查三角函数的图象,定积分.将的图象向右平移个单位后得到=;令,在上解得或;所以所围成的...