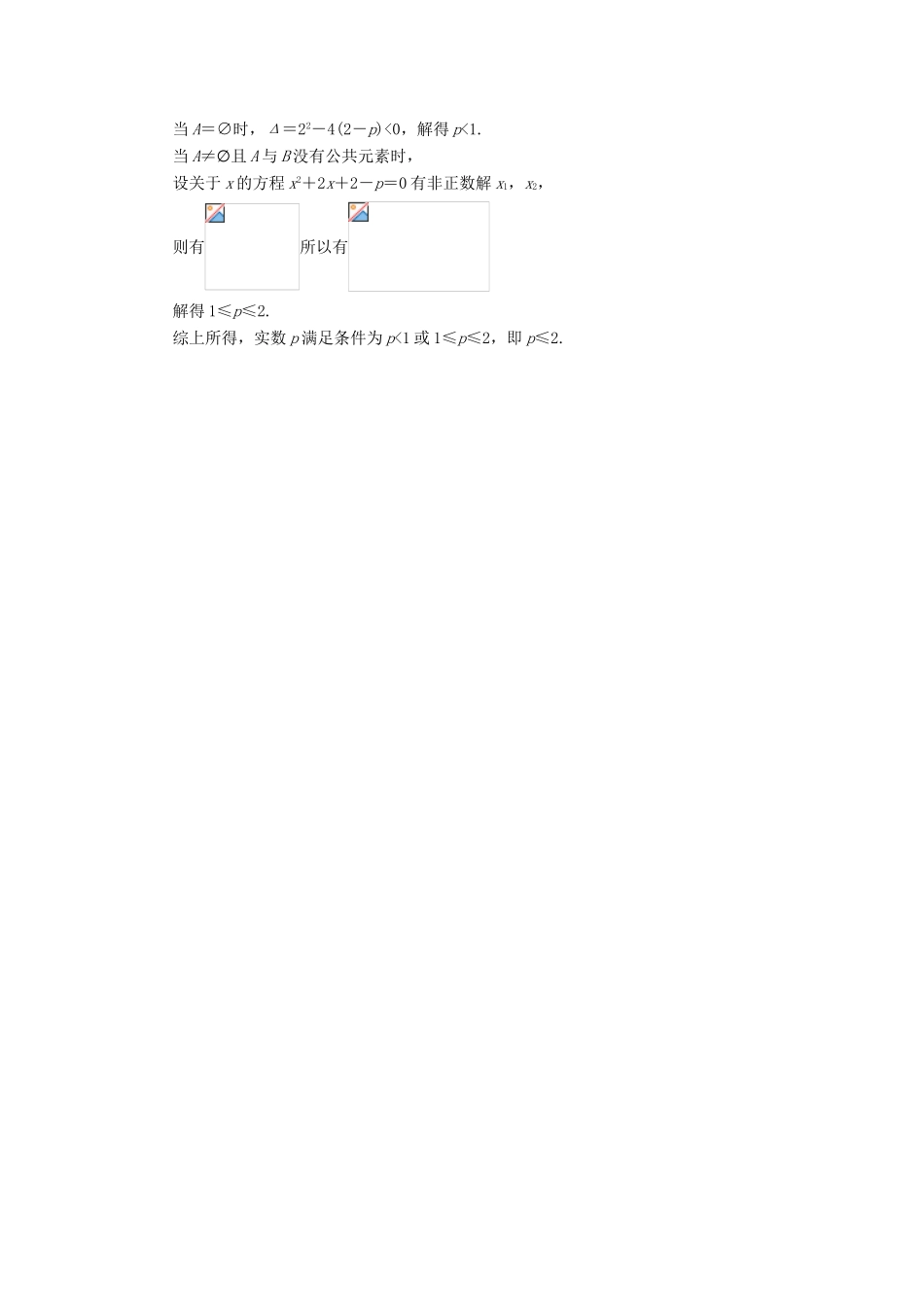
1.2.2集合的运算课堂探究探究一两个集合的交集运算求两个集合的交集时,首先要识别所给集合,其次要简化集合,即明确集合中的元素,使集合中的元素明朗化,最后再依据交集的定义写出结果.有时要借助于Venn图或数轴写出交集.【典型例题1】设A={x|x2-7x+6=0},B={x|40},B={x|-20的解集,再借助于数轴写出A∪B.解:A={x|x>-1},在数轴上分别表示集合A,B,如图所示,由数轴可知A∪B={x|x>-2}.探究三集合运算性质的运用1.A∪B=A⇔B⊆A,A∩B=A⇔A⊆B,这两个性质常常作为“等价转化”的依据,要特别注意当A⊆B时,往往需要按A=∅和A≠∅两种情况分类讨论,而这一点却很容易在解题时被忽视,因此当题目中有A⊆B这一条件时,应有分类讨论的思想意识,以免造成漏解或增解.2.要注重集合语言与数学文字语言之间的转化.【典型例题3】集合A={x|x2-3x+2=0},B={x|mx-1=0},若A∪B=A,则实数m构成的集合为________.思路分析:解答此题,第一是先利用性质A∪B=A⇔B⊆A来转化;二是要弄清楚B={x|mx-1=0}≠,要注意对m是否为0进行讨论.解析:A={x|x2-3x+2=0}={1,2},A∪B=A⇔B⊆A.因此集合B只能为单元素集或∅.(1)当B={1}时,即1∈B={x|mx-1=0},得m=1;同理,当B={2}时,得m=.(2)当B=∅时,即mx-1=0无解,得m=0.综上(1)(2)可知,实数m构成的集合为.答案:探究四集合的交、并综合运算集合的交、并综合运算一般需要将所给集合进行求解,有方程问题、不等式问题、点集等,把集合明确后,根据集合的特点及集合的交集、并集运算的定义,选取合适的方法进行运算,如:可结合数轴、Venn图或初中所学函数的图象等.【典型例题4】已知集合A={y|y=x2-2x-3,x∈R},B={y|y=-x2+2x+13,x∈R},求A∩B,A∪B.思路分析:先利用配方法确定集合A与B,再利用数轴进行集合的交、并运算.解:∵A={y|y=(x-1)2-4,x∈R},∴A={y|y≥-4}.∵B={y|y=-(x-1)2+14,x∈R},∴B={y|y≤14}.将集合A,B分别表示在数轴上,如图所示,∴A∩B={y|-4≤y≤14},A∪B=R.点评本题在求A∩B时,极易出现由得y=5,近而得出A∩B={5}的错误.探究五易错辨析易错点忽视A不为空集的情况而致误【典型例题5】设集合A={x∈R|x2+2x+2-p=0},B={x|x>0},且A∩B=∅,求实数p满足的条件.错解:由于A∩B=∅,则A=∅,所以关于x的方程x2+2x+2-p=0没有实数根,所以Δ=22-4(2-p)<0,解得p<1.所以实数p满足的条件为p<1.错因分析:当A∩B=∅时,若B≠∅,则A=∅或A≠∅且A与B没有公共元素,错解忽视了B≠∅,且A与B没有公共元素的情况,导致出现错误.正解:由A∩B=∅,且B≠∅,得A=∅或A≠∅且A与B没有公共元素.当A=∅时,Δ=22-4(2-p)<0,解得p<1.当A≠∅且A与B没有公共元素时,设关于x的方程x2+2x+2-p=0有非正数解x1,x2,则有所以有解得1≤p≤2.综上所得,实数p满足条件为p<1或1≤p≤2,即p≤2.