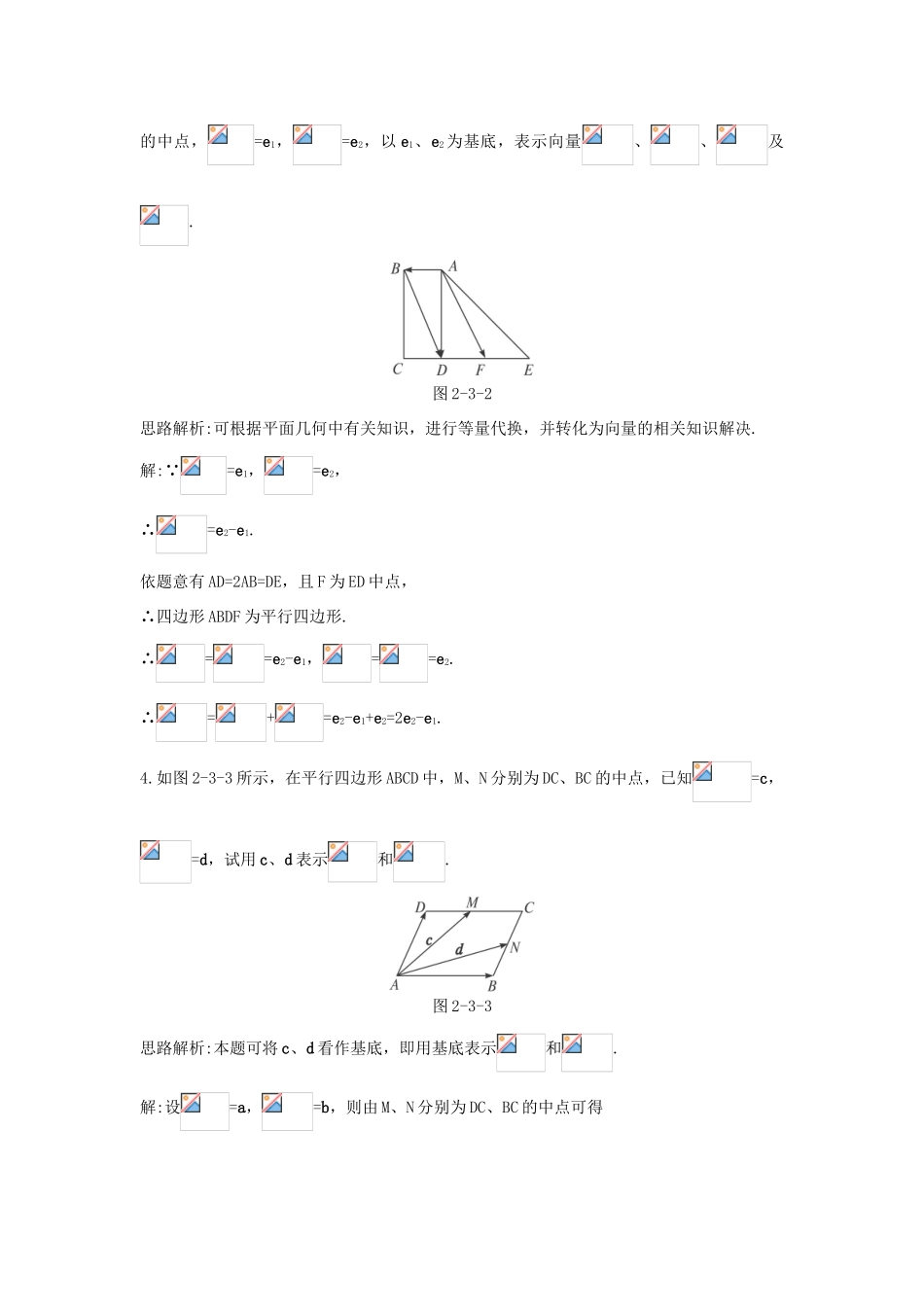
2.3.1平面向量基本定理5分钟训练(预习类训练,可用于课前)1.如图2-3-1所示,、不共线,=t(t∈R),用、表示.图2-3-1解:、不共线,则、可作基底,据定理有且只有一组实数λ1、λ2,使=λ1+λ2.2.向量、、的终点A、B、C在一条直线上,且=-3.设=p,=q,=r,则下列等式成立的是()A.r=-p+qB.r=-p+2qC.r=p-qD.r=-q+2p思路解析:由=-3,得-=-3(-),即2=-+3,∴=-+,即r=-p+q.答案:A10分钟训练(强化类训练,可用于课中)1.设一直线上三点A、B、P满足=λ(λ≠1),O是空间一点,则用、表示为()A.=+λB.=λ+(1-λ)C.=D.=+思路解析:由=λ(λ≠1),得-=λ(-),即=.答案:C2.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A、C),则等于()A.λ(+),λ∈(0,1)B.λ(+),λ∈(0,)C.λ(-),λ∈(0,1)D.λ(-),λ∈(0,)思路解析: 点P在对角线AC上,∴与共线.又=+,=λ(+).当P与A重合时,λ=0;当P与C重合时,λ=1.答案:A3.如图2-3-2所示,四边形ABCD为矩形,且AD=2AB,又△ADE为等腰直角三角形,F为ED的中点,=e1,=e2,以e1、e2为基底,表示向量、、及.图2-3-2思路解析:可根据平面几何中有关知识,进行等量代换,并转化为向量的相关知识解决.解: =e1,=e2,∴=e2-e1.依题意有AD=2AB=DE,且F为ED中点,∴四边形ABDF为平行四边形.∴==e2-e1,==e2.∴=+=e2-e1+e2=2e2-e1.4.如图2-3-3所示,在平行四边形ABCD中,M、N分别为DC、BC的中点,已知=c,=d,试用c、d表示和.图2-3-3思路解析:本题可将c、d看作基底,即用基底表示和.解:设=a,=b,则由M、N分别为DC、BC的中点可得=b,=a.从△ABN和△ADM中可得即=(2d-c),=(2c-d).志鸿教育乐园感想甲:听说你最近去美国考察了一次,感受不浅吧?乙:是啊,感触太深了,人家的文化水平就是高.甲:何以见得呢?乙:人家大人小孩都会说英语.30分钟训练(巩固类训练,可用于课后)1.(2005全国卷Ⅱ)已知向量=(k,12),=(4,5),=(-k,10),且A、B、C三点共线,则k=_________________.思路解析:三点共线,则任意两点连线的斜率相等.因为=(k,12),=(4,5),=(-k,10),所以A(k,12)、B(4,5)、C(-k,10).KAB=KBC,所以,解得k=-.答案:-2.(2005山东)已知向量a、b,且=a+2b,=-5a+6b,=7a-2b,则一定共线的三点是()A.A、B、DB.A、B、CC.B、C、DD.A、C、D思路解析:本题考查向量的概念及其运算.=+=2a+4b=2,∴A、B、D三点共线.答案:A3.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A、C),则等于()A.λ(+),λ∈(0,1)B.λ(+),λ∈(0,)C.λ(-),λ∈(0,1)D.λ(-),λ∈(0,)思路解析:如图,由向量的运算法则=+及点P在对角线AC上,所以与同向,且||<||,故=λ(+),λ∈(0,1).答案:A4.平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足=α+β,其中α、β∈R,且α+β=1,则点C的轨迹方程为()A.3x-2y-11=0B.(x-1)2+(y-2)2=5C.2x-y=0D.x+2y-5=0思路解析:由=α+β,α+β=1,知A、B、C三点共线.∴C点的轨迹是直线AB,由两点式得,即x+2y-5=0.答案:D5.如图2-3-4所示,在△ABC中,M是边AB的中点,E是CM的中点,AE的延长线交BC于F,MH∥AF.求证:==.图2-3-4证明:M为AB中点,MH∥AF,则=x.设=a,=b.=+x,=a+2x.又E为CM的中点,==.=b-,==.又=-=(a+2x)-(+).由+=,(a+2x)-(+)+()=b,+x+=b,3x=b-a,x=(b-a).==(b-a),而=(b-a)-(b-a)=(b-a).∴==.6.如图2-3-5所示,在平行四边形PQRS中,在PQ、QR、RS、SP上分别取点K、L、M、N,其中K、N分别为PQ、PS的中点,QL=QR,SM=SR,设KM与LN交于A点,=a,=q,=s,试用q、s表示a.图2-3-5思路解析:本题是求以q、s为一组基底的a的线性分解式.由于=+,而=,关键是.又由于与共线,而可用q、s表示,这样可以求得一个关于q、s的分解式(含参数).同样,利用、还可求得另一个关于q、s的分解式(也含参数).由于关于q、s的分解式的唯一性,就可得到含参数的两个方程,解出参数值,问题便可解决.解法一: 与共线,∴存在实数λ1,使=λ1. =,K为的中点,=,=-,=,∴=++(-)=-+,即=-q+s.∴=-q+λ1s. =+,K为的中点,∴=q-q+λ1s,即=(-)q+λ1s.同样设=λ2,==+-=-=q-s,∴=+=+λ2=s+λ2q-s=(-)s+λ2q. 关于q、s的分解式是唯一的,∴∴=q+s.解法二:由于N、A、L三点共线,故存在α...