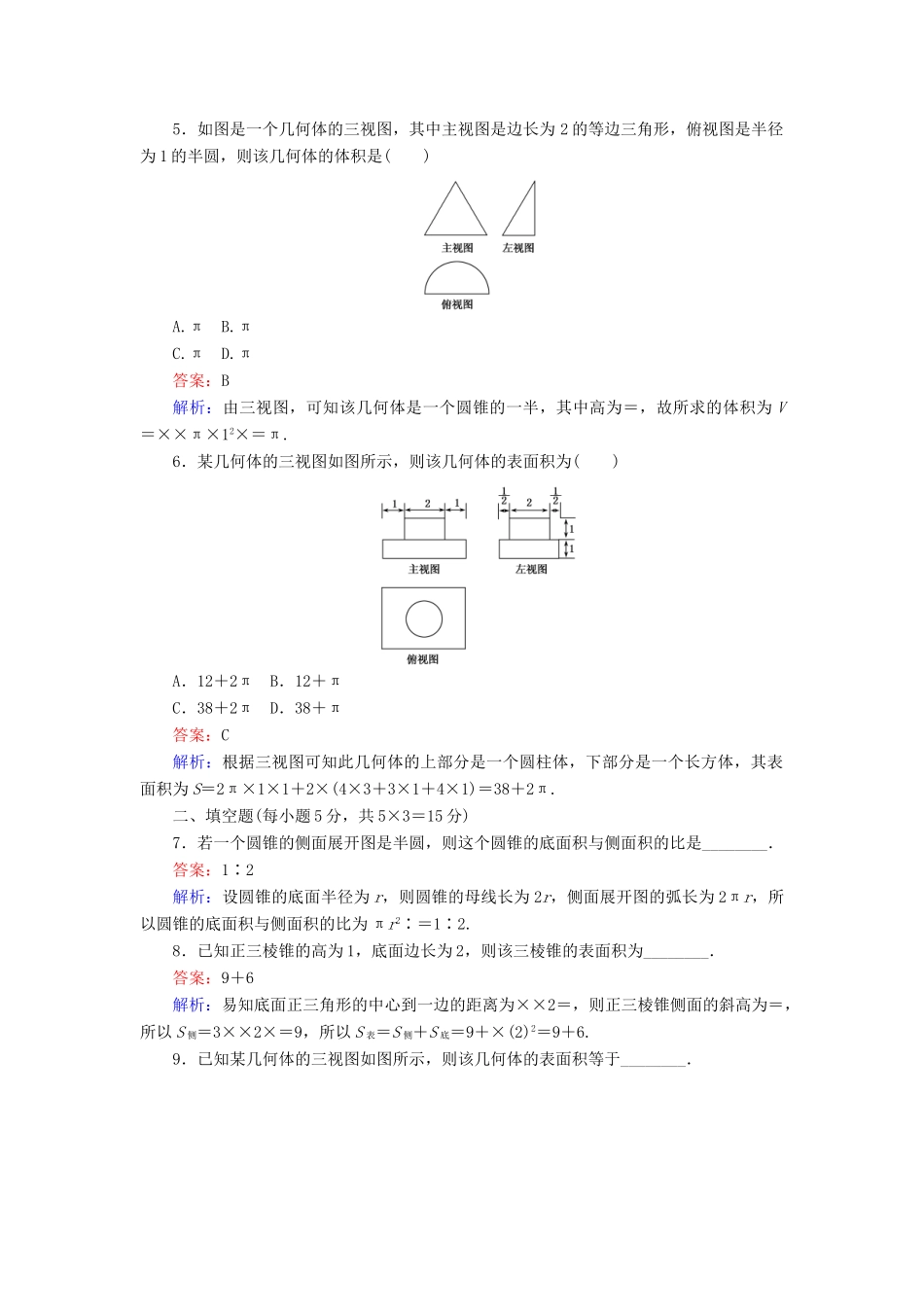
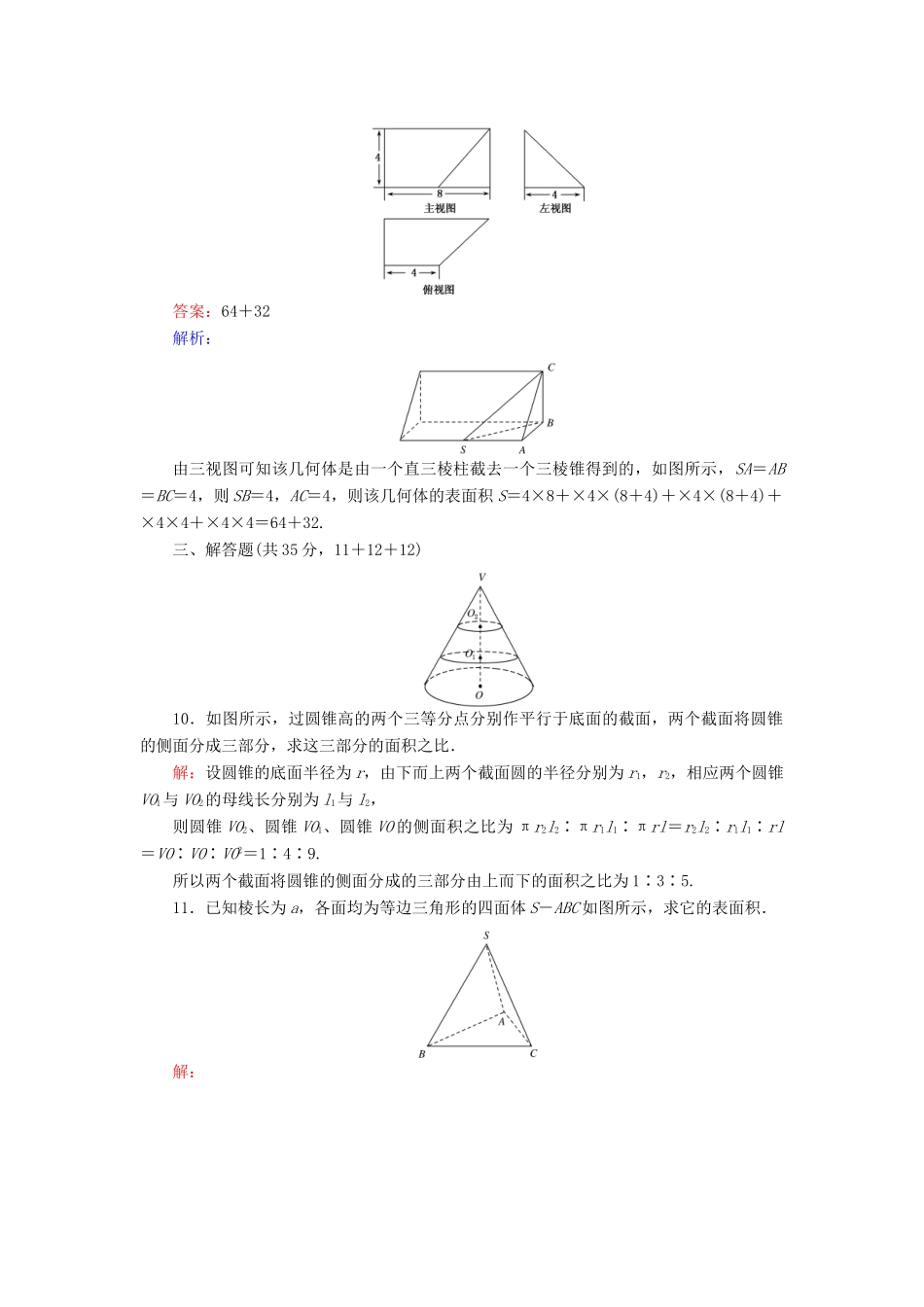
7.1简单几何体的侧面积时间:45分钟满分:80分班级________姓名________分数________一、选择题(每小题5分,共5×6=30分)1.若圆柱的底面面积为S,侧面展开图是一个正方形,则这个圆柱的侧面积是()A.4πSB.2πSC.πSD.πS答案:A解析:设圆柱的底面半径为r,则πr2=S,r=.又侧面展开图是正方形,所以圆柱的侧面积S侧=2=4πS.2.如图所示,圆锥的底面半径为1,高为,则该圆锥的表面积为()A.πB.2πC.3πD.4π答案:C解析:设圆锥的母线长为l,则l==2,所以圆锥的表面积为S=π×1×(1+2)=3π.3.已知正六棱柱的高为6,底面边长为4,则它的表面积为()A.48(3+)B.48(3+2)C.24(+)D.144答案:A解析:由题意,知侧面积为6×6×4=144,两底面积之和为2××42×6=48,所以表面积S=48(3+).4.正方体ABCD-A1B1C1D1中,以顶点A、C、B1、D1为顶点的正三棱锥的全面积为4,则该正方体的棱长为()A.B.2C.4D.2答案:A解析:设正方体棱长为a,侧面的对角线长为a,所以正三棱锥A-CB1D1的棱长为a,其表面积为4××(a)2=4,可得a2=2,即a=.5.如图是一个几何体的三视图,其中主视图是边长为2的等边三角形,俯视图是半径为1的半圆,则该几何体的体积是()A.πB.πC.πD.π答案:B解析:由三视图,可知该几何体是一个圆锥的一半,其中高为=,故所求的体积为V=××π×12×=π.6.某几何体的三视图如图所示,则该几何体的表面积为()A.12+2πB.12+πC.38+2πD.38+π答案:C解析:根据三视图可知此几何体的上部分是一个圆柱体,下部分是一个长方体,其表面积为S=2π×1×1+2×(4×3+3×1+4×1)=38+2π.二、填空题(每小题5分,共5×3=15分)7.若一个圆锥的侧面展开图是半圆,则这个圆锥的底面积与侧面积的比是________.答案:1∶2解析:设圆锥的底面半径为r,则圆锥的母线长为2r,侧面展开图的弧长为2πr,所以圆锥的底面积与侧面积的比为πr2∶=1∶2.8.已知正三棱锥的高为1,底面边长为2,则该三棱锥的表面积为________.答案:9+6解析:易知底面正三角形的中心到一边的距离为××2=,则正三棱锥侧面的斜高为=,所以S侧=3××2×=9,所以S表=S侧+S底=9+×(2)2=9+6.9.已知某几何体的三视图如图所示,则该几何体的表面积等于________.答案:64+32解析:由三视图可知该几何体是由一个直三棱柱截去一个三棱锥得到的,如图所示,SA=AB=BC=4,则SB=4,AC=4,则该几何体的表面积S=4×8+×4×(8+4)+×4×(8+4)+×4×4+×4×4=64+32.三、解答题(共35分,11+12+12)10.如图所示,过圆锥高的两个三等分点分别作平行于底面的截面,两个截面将圆锥的侧面分成三部分,求这三部分的面积之比.解:设圆锥的底面半径为r,由下而上两个截面圆的半径分别为r1,r2,相应两个圆锥VO1与VO2的母线长分别为l1与l2,则圆锥VO2、圆锥VO1、圆锥VO的侧面积之比为πr2l2∶πr1l1∶πrl=r2l2∶r1l1∶rl=VO∶VO∶VO2=1∶4∶9.所以两个截面将圆锥的侧面分成的三部分由上而下的面积之比为1∶3∶5.11.已知棱长为a,各面均为等边三角形的四面体S-ABC如图所示,求它的表面积.解:因为四面体S-ABC的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面面积的4倍.不妨求△SBC的面积,过点S作SD⊥BC,交BC于点D,如图所示.因为BC=SB=a,SD===a,所以S△SBC=BC·SD=a×a=a2.故四面体S-ABC的表面积S=4×a2=a2.12.已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱.(1)求圆柱的侧面积;(2)x为何值时,圆柱的侧面积最大.解:(1)画圆锥及内接圆柱的轴截面(如图所示),设所求的圆柱的底面半径为r,它的侧面积S圆柱侧=2πrx.∵=,(由相似三角形可知)∴r=R-·x,∴S圆柱侧=2πRx-·x2.(2)因为S圆柱侧的表达式中x2的系数小于零,所以这个二次函数有最大值.这时圆柱的高是x=-=,当圆柱的高是已知圆锥的高的一半时,它的侧面积最大.