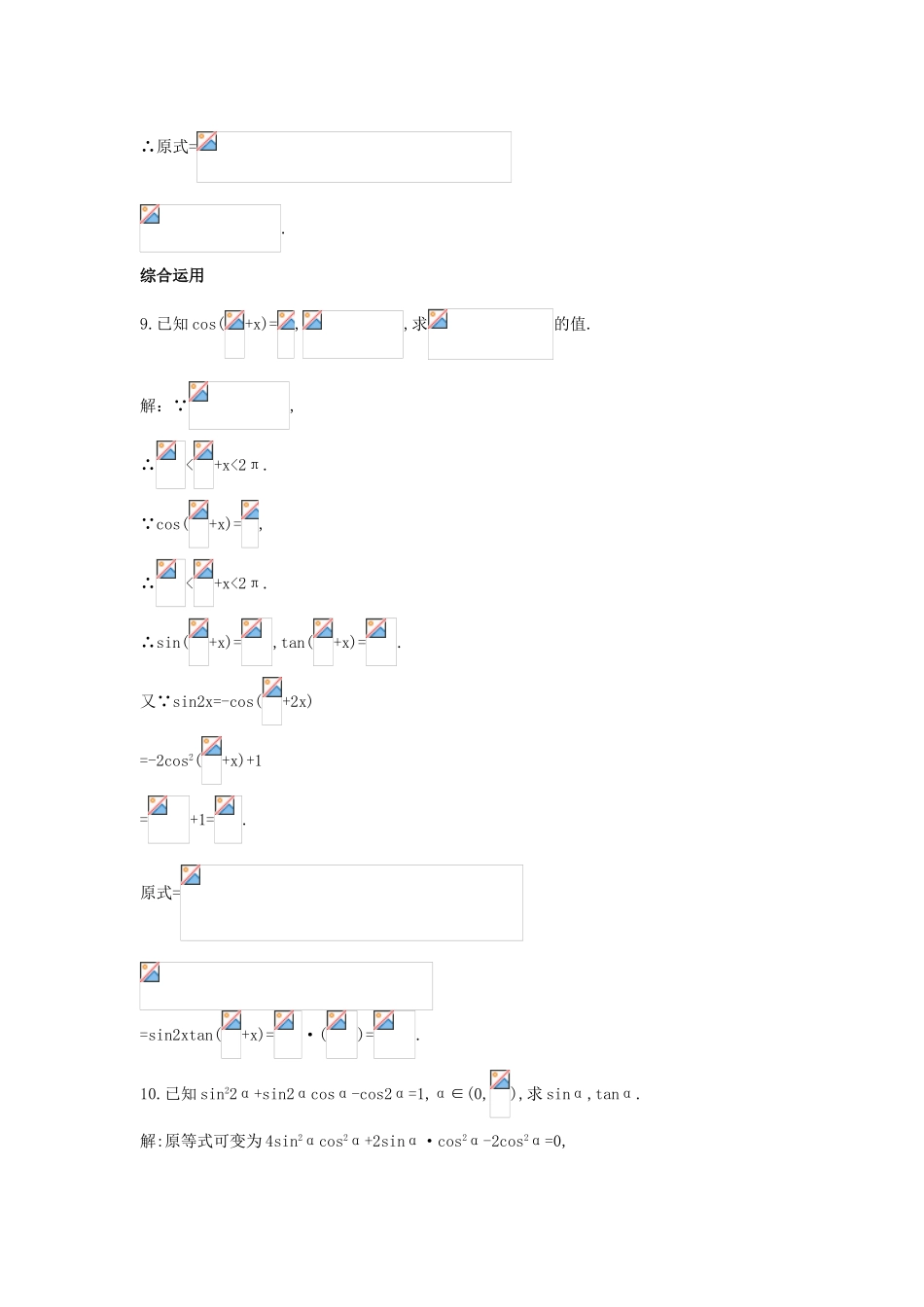
3.2.1倍角公式课后导练基础达标1.sinα-cosα=,则sin2α的值是()A.B.C.D.解析:两边平方,1-2sinαcosα=5,∴sin2α=.答案:B2.已知tanα+=m,则sin2α等于()A.B.C.2mD.解析:切化弦=m,∴sin2α=.答案:B3.cos·cos·cos·cos的值为()A.B.C.D.解析:乘以,利用倍角公式化简得.答案:D4.下列结论错误的是()A.tanα+B.tanα-C.sin2α-sin2β=sin(α+β)sin(α-β)D.1+cos2θ=2sin2θ解析:cos2θ=1-2sin2θ,∴2sin2θ=1-cos2θ.答案:D5.已知sinα=,则sin2(α-)=_____________.解析:原式=-cos2α(诱导公式).答案:2-6.化简.解:原式==sin50°+cos50°-(sin50°-cos50°)=2cos50°.7.已知sin(+x)sin(-x)=,x∈(,π),求sin4x的值.解:∵sin(+x)sin(-x)=sin(+x)sin[-(+x)]=sin(+x)cos(+x)=sin(+2x)=cos2x=,∴cos2x=.∵x∈(,π),∴2x∈(π,2π).∴sin2x=.∴sin4x=2sin2xcos4x=.8.已知tan(+θ)=3,求sin2θ-2cos2θ的值.解:∵tan(+θ)==3,∴tanθ=.∴原式=.综合运用9.已知cos(+x)=,,求的值.解:∵,∴<+x<2π.∵cos(+x)=,∴<+x<2π.∴sin(+x)=,tan(+x)=.又∵sin2x=-cos(+2x)=-2cos2(+x)+1=+1=.原式==sin2xtan(+x)=·()=.10.已知sin22α+sin2αcosα-cos2α=1,α∈(0,),求sinα,tanα.解:原等式可变为4sin2αcos2α+2sinα·cos2α-2cos2α=0,∴2cos2α(2sinα-1)(sinα+1)=0.∵α∈(0,),∴sinα+1≠0,cos2α≠0.∴sinα=,α=.∴tanα=11.α,β是锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0,求证:α+2β=.证明:由已知得3sin2α=1-2sin2β=cos2β,又sin2β=sin2α=3sinαcosα,∴cos(α+2β)=cosαcos2β-sinαsin2β=cosα3sin2α-sinα3sinαcosα=0.又0<α<,0<β<,∴0<α+2β<π.∴α+2β=.拓展探究12.如图,在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m至点C处测得顶端A的仰角为2θ,再继续前进m至D处,测得顶端A的仰角为4θ.同学们能否依据所测得的数据,计算出θ的大小与建筑物AE的高吗?解:由已知BC=30m,CD=10m.在Rt△ABE中,BE=AEcotθ,在Rt△ACE中,CE=AEcot2θ,∴BC=BE-CE=AE(cotθ-cot2θ),同理,可得CD=CE-DE=AE(cot2θ-cot4θ),∴,即.而=2cos2θ=,∴2cos2θ=cos2θ=2θ=30°.∴θ=15°,∴AE=AC=BC=15m.故θ为15°,建筑物高为15m.