高一数学正切函数的图象和性质、三角函数的应用苏教版VIP免费

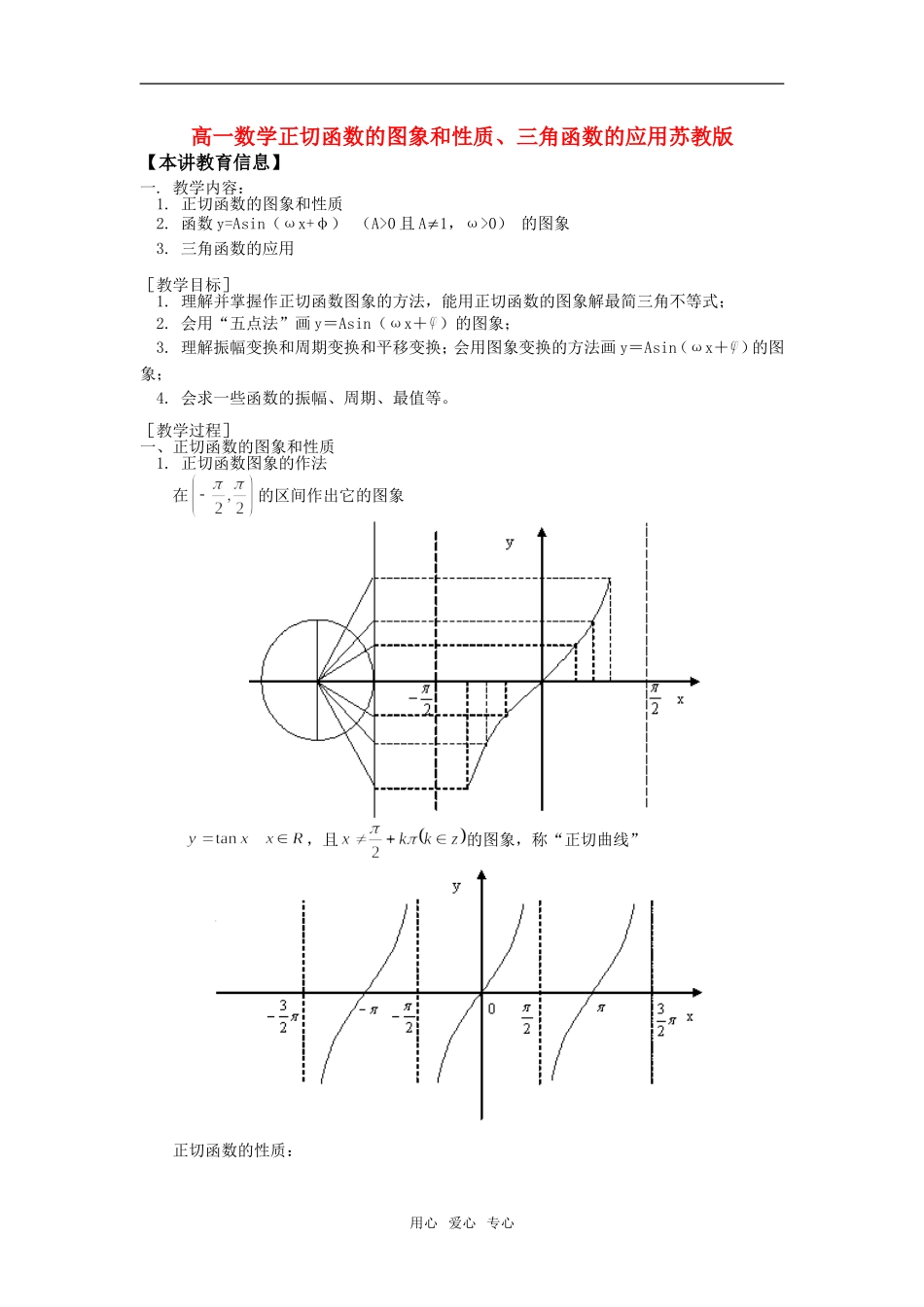
高一数学正切函数的图象和性质、三角函数的应用苏教版【本讲教育信息】一.教学内容：1.正切函数的图象和性质2.函数y=Asin（ωx+φ）（A>0且A1，ω>0）的图象3.三角函数的应用［教学目标］1.理解并掌握作正切函数图象的方法，能用正切函数的图象解最简三角不等式；2.会用“五点法”画y＝Asin（ωx＋）的图象；3.理解振幅变换和周期变换和平移变换；会用图象变换的方法画y＝Asin（ωx＋）的图象；4.会求一些函数的振幅、周期、最值等。［教学过程］一、正切函数的图象和性质1.正切函数图象的作法在的区间作出它的图象，且的图象，称“正切曲线”正切函数的性质：用心爱心专心1.定义域：2.值域：R3.当时，当时4.周期性：5.奇偶性：奇函数6.单调性：在开区间内，函数单调递增二、函数y=Asin（ωx+φ）（A>0且A1，ω>0）的图象（一）函数图象的三种变换1.振幅变换y=Asinx，xR（A>0且A1）的图象可以看作把正弦曲线上的所有点的纵坐标变为原来的A倍而得到。A称为振幅（物体振动时离开平衡位置的最大距离）。2.周期变换:函数y=sinωx，xR（ω>0且ω1）的图象，可看作把正弦曲线上所有点的横坐标变到原来的倍（纵坐标不变）。ω决定了函数的周期。3.相位变换:函数y＝sin（x＋），x∈R（其中≠0）的图象，可以看作把正弦曲线上所有点向左（当＞0时）或向右（当＜0时）平行移动｜｜个单位长度而得到。【典型例题】例1.比较与的大小解：，，又内单调递增，例2.求函数的定义域、值域，并指出它的周期性、奇偶性、单调性解：由得，所求定义域为值域为R，周期，是非奇非偶函数在区间上是增函数用心爱心专心例3.观察正切曲线写出满足下列条件的x的值的范围：tanx＞0解：画出y＝tanx在（－，）上的图象，不难看出在此区间上满足tanx＞0的x的范围为：0＜x＜结合周期性，可知在x∈R，且x≠kπ＋上满足的x的取值范围为（kπ，kπ＋）（k∈Z）例4.画出函数y＝3sin（2x＋），x∈R的简图解：（五点法）由T＝，得T＝π列表：X–2x+0π2π3sin（2x+）030–30描点画图：这种曲线也可由图象变换得到：例5.已知函数y＝Asin（ωx＋），在同一周期内，当x＝时函数取得最大值2，当x＝时函数取得最小值－2，则该函数的解析式为（）用心爱心专心A.y＝2sin（3x－）B.y＝2sin（3x＋）C.y＝2sin（＋）D.y＝2sin（－）解析：由题设可知，所求函数的图象如图所示，点（，2）和点（，－2）都是图象上的点，且由“五点法”作图可知，这两点分别是“第二点”和“第四点”所以应有：解得：答案：B例6.一半径为3m的水轮如图所示，水轮圆心O距离水面2m，已知水轮每分钟转动4圈，如果当水轮上P点从水中浮现时（图中P0点）开始计算时间。（1）求P点相对于水面的高度z（m）与时间t（s）之间的函数关系式；（2）P点第一次到达最高点大约要多长时间？解：（1）设z=Asin（ωt+φ）+k由题意，知，又当t=0时，z=0，可得取=，解得故点P第一次到达最高点大约需要5.5s用心爱心专心【模拟试题】1.判断正误①y＝Asinωx的最大值是A，最小值是－A②y＝Asinωx的周期是③y＝-3sin4x的振幅是3，最大值为3，最小值是-32.下列变换中，正确的是A.将y＝sin2x图象上的横坐标变为原来的2倍（纵坐标不变）即可得到y＝sinx的图象B.将y＝sin2x图象上的横坐标变为原来的倍（纵坐标不变）即可得到y＝sinx的图象C.将y＝-sin2x图象上的横坐标变为原来的倍，纵坐标变为原来的相反数，即得到y＝sinx的图象D.将y＝-3sin2x图象上的横坐标缩小一倍，纵坐标扩大到原来的倍，且变为相反数，即得到y＝sinx的图象3.函数y＝tan（ax＋）（a≠0）的最小正周期为（）4.函数y＝＋的定义域是（）A.（2k＋1）π≤x≤（2k＋1）π＋，k∈ZB.（2k＋1）π＜x＜（2k＋1）π＋，k∈ZC.（2k＋1）π≤x＜（2k＋1）π＋，k∈ZD.（2k＋1）π＜x＜（2k＋1）π＋或x＝kπ，k∈Z5.已知如图是函数y＝2sin（ωx＋）其中｜｜＜的图象，那么（）A.ω＝，＝B.ω＝，＝－C.ω＝2，＝D.ω＝2，＝－6.函数y＝tan（2x＋）的图象被平行直线隔开，与x轴交点的坐标是_________。与y轴交点的坐标是_________________，周期是___，定义域的集合是_____用心爱心专心__________，值域的集合是，...