参赛课件实际问题与反比例函数1VIP免费

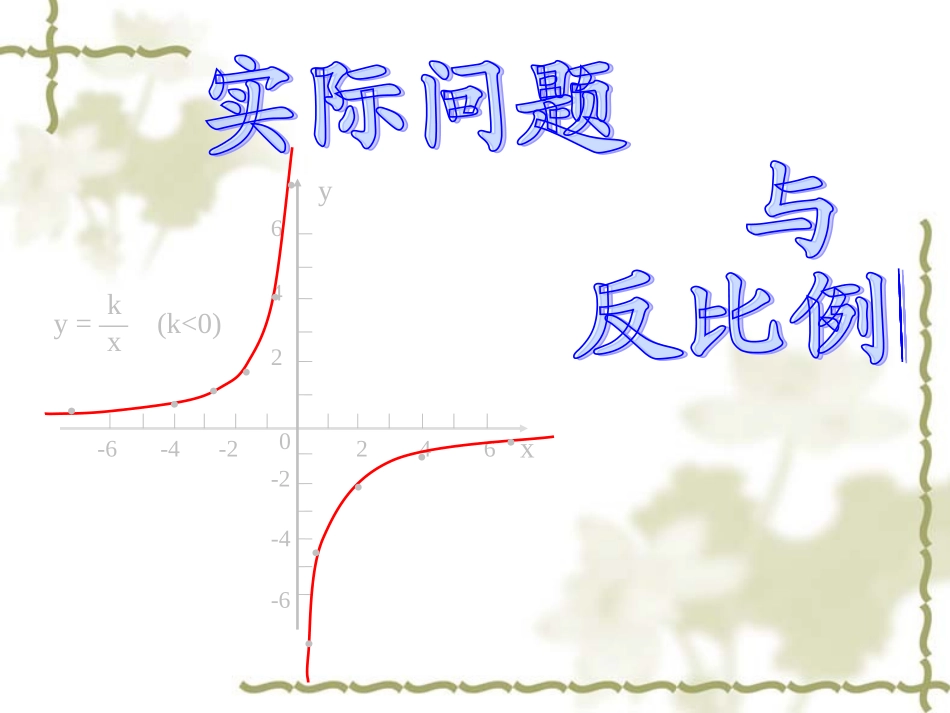
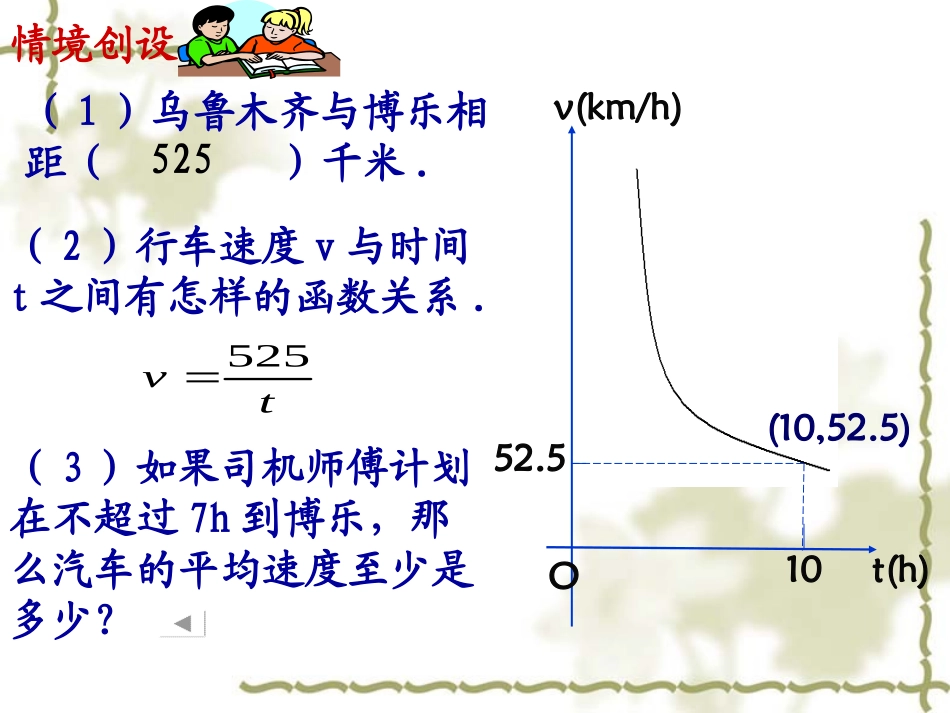
246246-6-4-20yx-2-4-6...．．．.．.．．y=—(k<0)kx亲爱的同学们：你们好！我是来自乌鲁木齐建工师二中的黄老师，很高兴见到你们，能与大家共同探讨实际问题与反比例函数这一话题我感到十分荣幸。听说博乐是个干净又美丽的城市，我又是第一次来，一路上心情十分激动、迫切想要快点到达！我在心里想：“如果司机师傅能开得稍微快一点，我就能早点到达了。”结果，我如愿以偿！同学们，在我所叙述的这个过程中藏着一对成反比例关系的变量，你们能试着找出来吗？（1）乌鲁木齐与博乐相距（）千米.（2）行车速度v与时间t之间有怎样的函数关系.情境创设tv525525（3）如果司机师傅计划在不超过7h到博乐，那么汽车的平均速度至少是多少？t(h)v(km/h)52.510(10,52.5)Ovt5257525v(3)由变形得tv525t(h)v(km/h)52.510(10,52.5)O∴汽车的平均速度至少为75km/h当t≤7时，即∵ｖ＞０∴525≤7v解得v≥75t(h)v(km/h)52.510(10,52.5)O(3)当t=7时，v=525÷7=75∴汽车的平均速度至少为75km/h应用迁移l一定体积的面团做成拉面，拉面总长度（cm）是拉面粗细（横截面积）S（）的反比例函数.2cm…………l拉面总长（cm）横截面积S()2cm体积为128的面团,拉面总长度（cm）与拉面粗细（横截面积）S（）的函数关系式为:lsl1282cm3cm同学们，你们已经帮助老师发现了一些生活中的变量之间存在的反比关系，在我们丰富多彩的生活中，一定还存在许多这样的例子.你们能再举出一些吗？小组合作、自我提升y(mg)x(min)86O为了预防“甲型H1N1流感”，学校对教室采用药熏消毒法进行消毒。巩固提高（1）药物燃烧时，y与x的关系式为：（2）药物燃烧后，y与x的关系式为：xy75.0）＜（80x）（848xxy请根据题中所提供的信息，解答下列问题：已知药物燃烧时，室内每立方米空气中的含药量y(mg)与时间x(min)成正比例，药物燃烧完后，y与x成反比例.现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg.(1)解：设药物燃烧阶段函数解析式为由题意得：∴此阶段函数解析式为）（011kxky75.08611kkxy75.0）＜（80xy(mg)x(min)86O(2)设药物燃烧结束后函数解析式为)0(22kxky由题意得：488622kk∴此阶段函数解析式为xy48)8(xy(mg)x(min)86O（3）当空气中每立方米的含药量低于1.6mg时学生方可进入教室是指药物燃烧完毕后∴当y=1.6时，6.148x即从消毒开始，至少经过30min后，学生才能回到教室；解得：x=30（3）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进入教室，那么从药物燃烧开始，至少经过______min后，学生才能回到教室；30y(mg)x(min)86301.6（4）当y=3时，0.75x=3得x=4即药物燃烧至第4分钟时空气中的含药量达到3mg348x得x=16即从药物燃烧开始--完毕直至第16分钟时空气中的含药量达到3mg在这个过程中，药量不低于3mg的时间为：164=12–（min）∵12＞10（4）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？请说明理由。∴此次消毒有效y(mg)x(min)864163…………“数与形，本是相倚相依，焉能分作两边飞.数缺形时少直觉，形少数时难入微.形数结合百般好，割裂分家万事非”------华罗庚数形结合，是我们数学学习中一种很重要的思想方法。同学们一定要灵活运用哦！