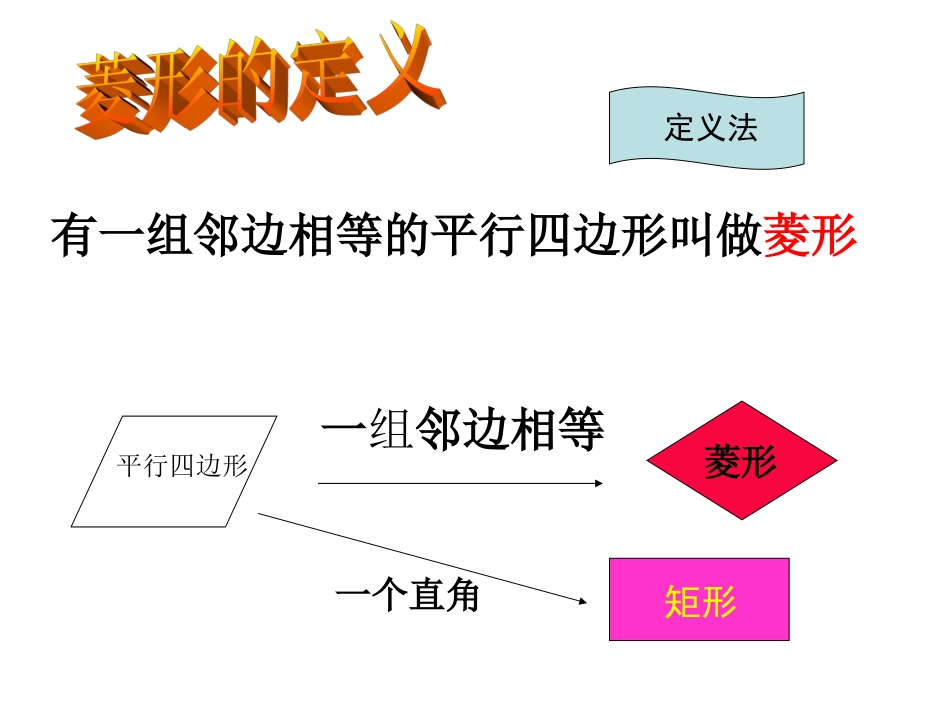
有一组邻边相等的平行四边形叫做菱形平行四边形一组邻边相等菱形定义法矩形一个直角菱形的性质1:菱形的四条边都相等。ABDC菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质的研究AB=BC=CD=AD菱形的性质2:菱形的两条对角线互相垂直,每一条对角线平分一组对角。ADCBO已知:在菱形ABCD中,对角线AC,BD相交于点O.求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.ADCBDAC,BDACOBDAC,DCDAABCD平分的中点是互相平分对角线是菱形四边形ABCD由此你能得出菱形的的对称性吗?两条对角线互相平分且垂直对边平行且相等边对角线角四条边都相等菱形的对角相等,邻角互补每一条对角线平分一组对角ADCBO对称性中心对称:对角线的交点就是对称中心轴对称:有两条对称轴即:两条对角线所在的直线相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BCOA=OCOB=OD∠DAB=BCDABC=CDA∠∠∠∠AOB=DOC=AOD=BOC=90°∠∠∠∠1=23=45=67=8∠∠∠∠∠∠∠△ABCDBCACDABD△△△RtAOBRtBOCRtCOD△△△RtDOA△RtAOBRtBOCRtCODRtDOA△≌△≌△≌△△ABDBCDABCACD≌△△≌△ABCDO12345678==1.菱形具有而矩形不一定有的性质是()(A)对角线互相平分(B)四条边都相等(C)对角相等(D)邻角互补牛刀小试ABCDEF122.已知:如图,在菱形ABCD中,直线AE交边BC于点E,直线AF交CD于点F,且BE=DF求证:21B【菱形的面积公式】ABCDE菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形的面积吗?S菱形=BC.AE思考:计算菱形的面积除了上述方法外,利用对角线能计算菱形的面积吗?BCDABDSSACBD21S菱形ABCD==面积:S菱形=底×高=对角线乘积的一半O判定方法1:有一组邻边相等的平行四边形是菱形∵四边形ABCD是平行四边形AB=BC∴四边形ABCD是菱形ABCD菱形判定方法的研究判定定理2对角线互相垂直的平行四边形是菱形已知ABCD中,对角线AC、BD互相垂直,求证:四边形ABCD是菱形.证明:在中,OA=OC(①).又∵ACBD⊥,∴BD所在直线是线段AC的垂直平分线,∴AB=BC,∴四边形ABCD是菱形(②).ABCD例已知:矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形证明∵四边形ABCD是矩形,∴AEFC∥(①)∴∠1=∠2.(②)∵EF平分AC,∴AO=OC.又∵∠AOE=∠COF=90°,∴△AOECOF≌△(③),∴EO=FO,∴四边形AFCE是平行四边形(④)又∵EFAC⊥,∴四边形AFCE是菱形(⑤)判定定理3:四条边都相等的四边形是菱形已知:AB=BC=CD=DA求证:四边形ABCD是菱形ABCD∵AB=CD,BC=AD∴四边形ABCD是平行四边形∵AB=CD∴四边形ABCD是菱形(有一组邻边相等的平行四边形是菱形)菱形常用的判定方法:①有一组邻边相等的平行四边形叫做菱形②对角线互相垂直的平行四边形是菱形③有四条边相等的四边形是菱形。+邻边相等=+对角线线互相垂直=四条边相等+=6已知:如图,AD平分∠BAC,DEAC∥交AB于E,DFAB∥交AC于F.求证:EFAD⊥;321ABCDEF当堂检测:1、判断下列说法是否正确?为什么?(1)对角线互相垂直的四边形是菱形;()(2)对角线互相垂直平分的四边形是菱形;()(3)对角线互相垂直,且有一组邻边相等的四边形是菱形;()╳√╳∟ADBC∟ABCD2、□ABCD的对角线AC与BD相交于点O,(1)若AB=AD,则□ABCD是形;(2)若AC=BD,则□ABCD是形;(3)若∠ABC是直角,则□ABCD是形;(4)若∠BAO=∠DAO,则□ABCD是形。ABCDO矩菱矩菱ADCB∟∟EF把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?课后拓展1:请你动脑筋如图,ADBC∥,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。CDBAO课后拓展2:┐)12(提示:AODCOB△≌△(角边角)AD=BC