平面与平面垂直的性质VIP免费

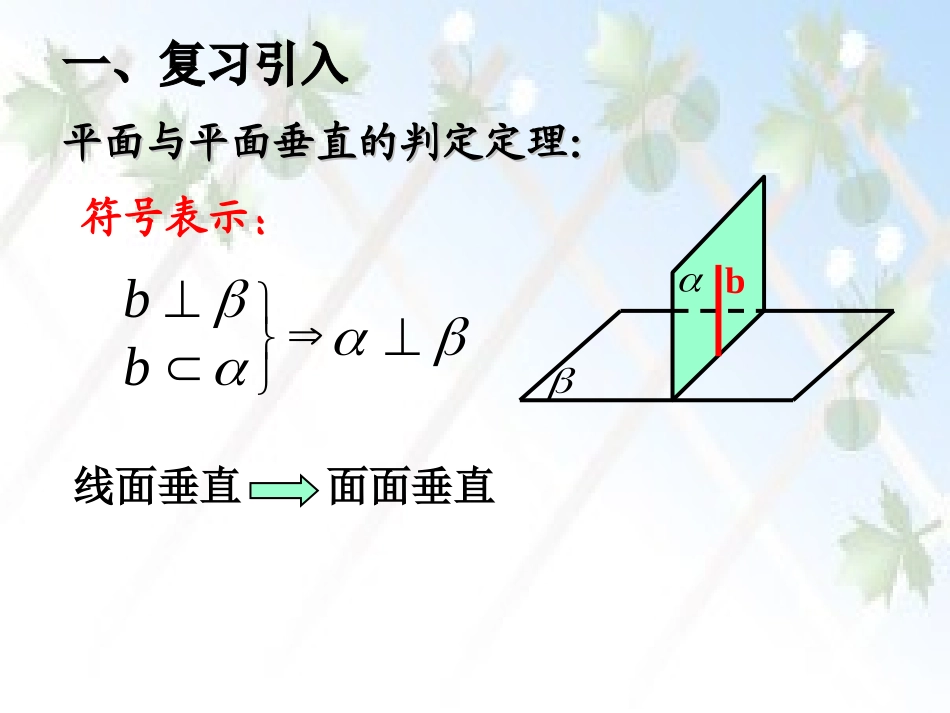
lb平面与平面垂直的判定定理：平面与平面垂直的判定定理：b面面垂直线面垂直符号表示：bb如果将中的条件与结论的位置调换，构造这样的一个命题：b该命题正确吗？bbbbⅠ.观察实验不一定lb（1）观察模型，平面与平面是互相垂直的，那么平面内的任意一条直线是否就一定与平面垂直？（2）记与平面垂直的直线为b,平面与平面的交线为，则b与满足什么关系？lllbbⅡ.概括结论llbblb则∠AOB就是二面角--的平面角∵,又∵b⊥,且OB是平面内两条相交直线证明:设b=OA,在平面内作OB⊥于点O,∴b⊥Ⅲ.证明lbAOBl90AOBlllbllbb∴OAOB,⊥即b⊥OB与lbllbbb两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.简述为：面面垂直线面垂直符号表示：平面与平面垂直的性质定理定理剖析：定理剖析：前提：两面垂直①线在平面内②线垂直于交线关键：应用：①判定线面垂直②作平面的垂线×四、知识应用举例例1：1.已知：.判断下列命题是否正确：×.,)1(bb则若.,,)2(blbl则若×内的垂直于平面则若bb,)3(.无数条直线√任意一条lbaa2.已知：.直线满足,若aa则直线与平面的位置关系为：aa//a,abl例2：如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，平面PAC⊥平面ABC.BOPAC求证：BC⊥平面PAC.证明：AB是⊙O的直径，C是圆周上不同于A，B的任意一点BCAC⊥面PAC面ABC=AC又BOPACBC⊥面PAC面PAC⊥面ABC，BC面ABC证明：AB是⊙O的直径，C是圆周上不同于A，B的面PAC⊥面ABC，BOPACD过点P作PDAC⊥于点D.面PAC面ABC=ACPD⊥面ABCBC面ABCPDBC⊥任意一点ACBC⊥又PD与AC是面PAC内两条相交直线BC⊥面PAC又例2：如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，平面PAC⊥平面ABC.BOPAC拓展1：求证：BC⊥平面PAC.判断平面PBC与平面PAC是否垂直，并说明理由.证明:平面PBC⊥平面PACBC⊥面PACBC面PBC平面PBC⊥平面PACBOPAC已知：平面ABC⊥平面PAC，平面PBC⊥平面PAC.判断BC与平面PAC是否垂直？拓展2：BPACBC⊥面PAC证明：取面PAC内任一点O,过点O作ODPC⊥于点D，OEAC⊥于点E.面PBC⊥面PAC，面PBC面PAC=PCOD⊥面PBCBPACODEBC面PBCODBC⊥同理可证：OEBC⊥OD、OE是面PAC内两条相交直线BC⊥面PAC已知：平面ABC⊥平面PAC，平面PBC⊥平面PAC.证明：BC⊥面PAC2、平面与平面垂直的性质定理主要应用来解决什么问题？1、这节课我们主要学习了哪些内容？①判定线面垂直②作平面的垂线课本课本P74P74：习题：习题BB组第组第33题题作业备选练习题如图，四棱锥PABCD的底面是矩形，2,2,ABBCPAB侧面是等边三角形，且侧PAB面底面ABCD.(1).证明：PAB面面PBC.(2).求PC与底面ABCD所成的角.PABCD