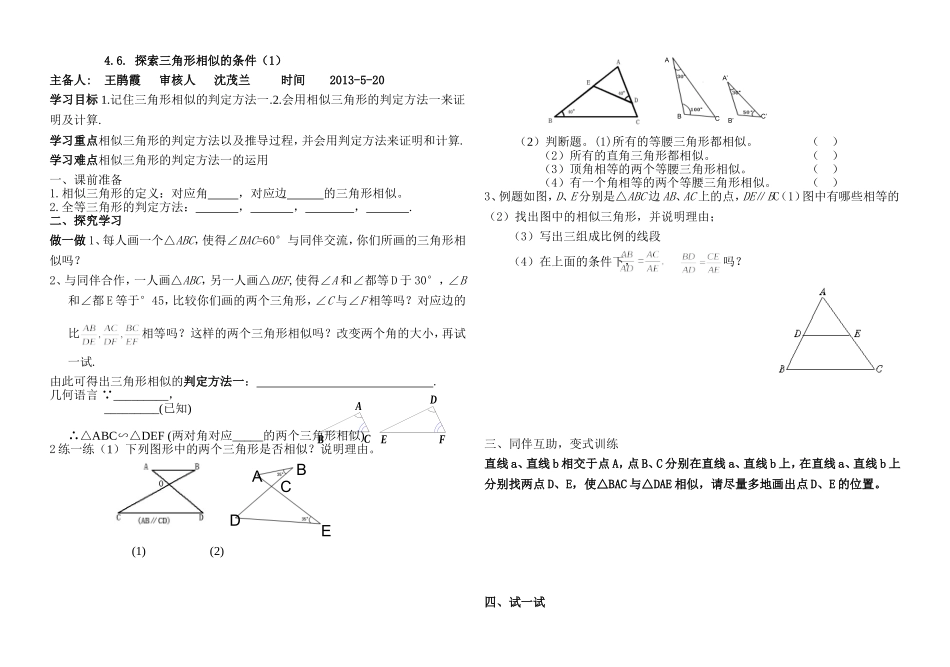
4.6.探索三角形相似的条件(1)主备人:王鹃霞审核人沈茂兰时间2013-5-20学习目标1.记住三角形相似的判定方法一.2.会用相似三角形的判定方法一来证明及计算.学习重点相似三角形的判定方法以及推导过程,并会用判定方法来证明和计算.学习难点相似三角形的判定方法一的运用一、课前准备1.相似三角形的定义:对应角,对应边的三角形相似。2.全等三角形的判定方法:,,,.二、探究学习做一做1、每人画一个△ABC,使得∠BAC=60°与同伴交流,你们所画的三角形相似吗?2、与同伴合作,一人画△ABC,另一人画△DEF,使得∠A和∠都等D于30°,∠B和∠都E等于°45,比较你们画的两个三角形,∠C与∠F相等吗?对应边的比相等吗?这样的两个三角形相似吗?改变两个角的大小,再试一试.由此可得出三角形相似的判定方法一:.几何语言∵_________,_________(已知)∴△ABC∽△DEF(两对角对应_____的两个三角形相似)2练一练(1)下列图形中的两个三角形是否相似?说明理由。(1)(2)(2)判断题。(1)所有的等腰三角形都相似。()(2)所有的直角三角形都相似。()(3)顶角相等的两个等腰三角形相似。()(4)有一个角相等的两个等腰三角形相似。()3、例题如图,D、E分别是△ABC边AB、AC上的点,DE∥BC(1)图中有哪些相等的(2)找出图中的相似三角形,并说明理由;(3)写出三组成比例的线段(4)在上面的条件下,吗?三、同伴互助,变式训练直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使△BAC与△DAE相似,请尽量多地画出点D、E的位置。四、试一试ABCDEABCA’B’C’ABCDEF观察到对面岸边的一个标志O,于是他想出了一个测量河宽的办法。他在自己的岸边选点A、B、D,使得AB⊥AO,DB⊥AB,然后确定DO和AB的交点C。然后测得AC=120米。CB=60米,BD=200米,你能帮助他算出莱茵河的宽度吗?五、小结通过本节课的学习,你有哪些收获我知道了…………我学会了…………我感到困难的是…………当堂检测1、如图,G是ABCD的CD延长线上一点,连结BC交对角线AC于E,交AD于F,则:(1)图中与△AEF相似的三角形有_______。(2)图中与△ABC相似的三角形有_______。(3)图中与△GFD相似的三角形有________。2、过△ABC(∠C>∠B)的边AB上一点D作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?请把它们一一作出来。