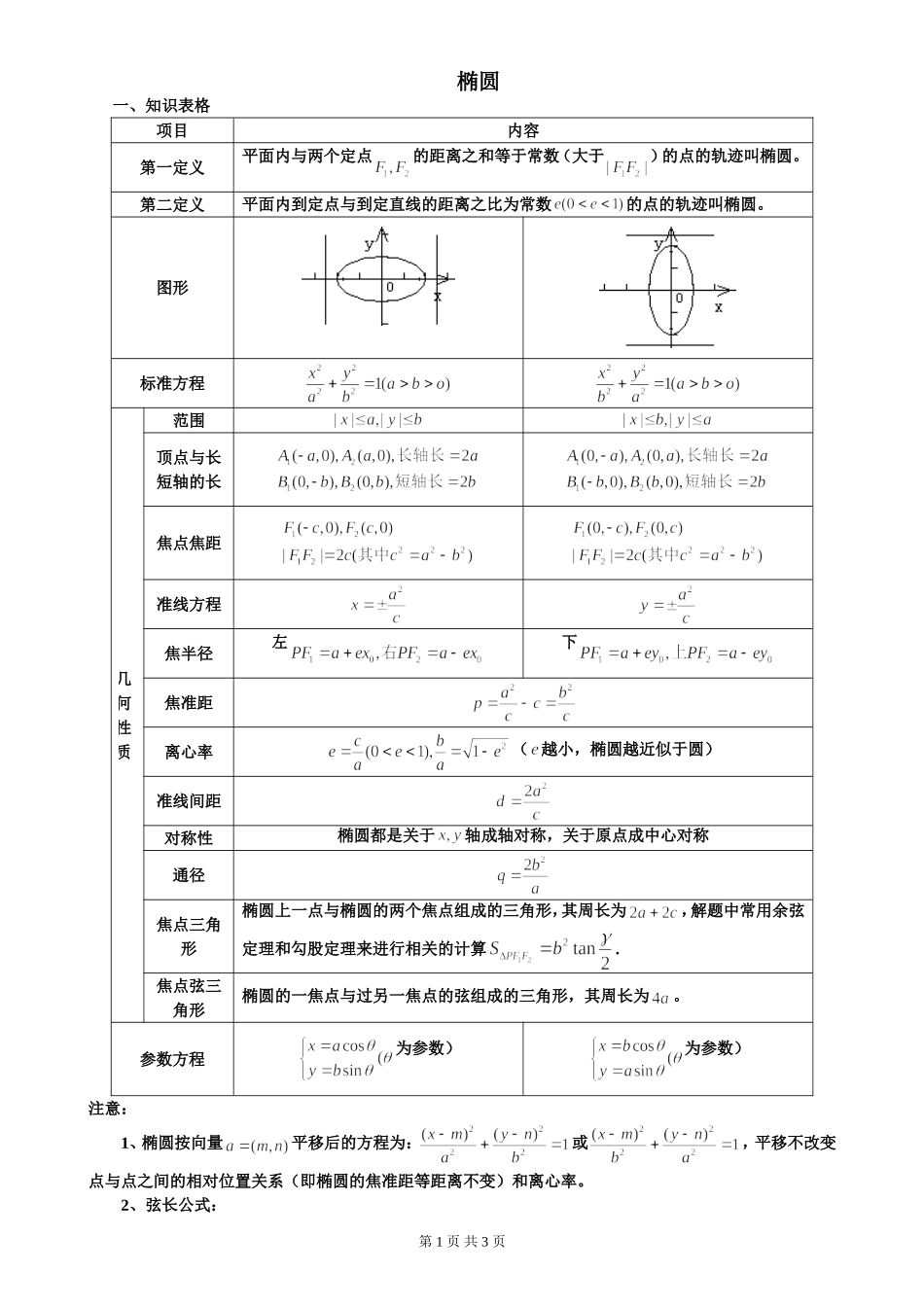
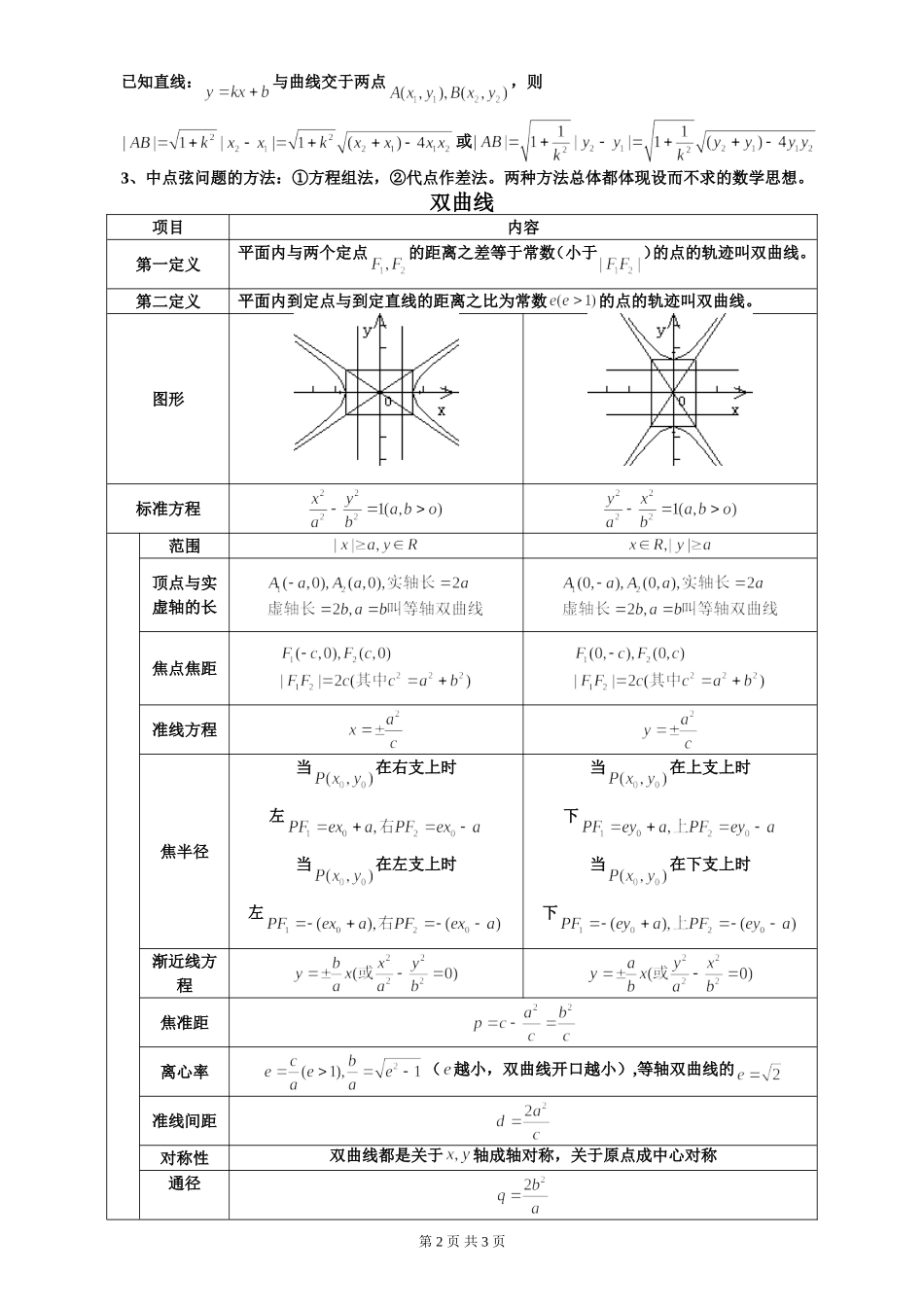
椭圆一、知识表格项目内容第一定义平面内与两个定点的距离之和等于常数(大于)的点的轨迹叫椭圆。第二定义平面内到定点与到定直线的距离之比为常数的点的轨迹叫椭圆。图形标准方程几何性质范围顶点与长短轴的长焦点焦距准线方程焦半径左下焦准距离心率(越小,椭圆越近似于圆)准线间距对称性椭圆都是关于轴成轴对称,关于原点成中心对称通径焦点三角形椭圆上一点与椭圆的两个焦点组成的三角形,其周长为,解题中常用余弦定理和勾股定理来进行相关的计算.焦点弦三角形椭圆的一焦点与过另一焦点的弦组成的三角形,其周长为。参数方程为参数)为参数)注意:1、椭圆按向量平移后的方程为:或,平移不改变点与点之间的相对位置关系(即椭圆的焦准距等距离不变)和离心率。2、弦长公式:第1页共3页已知直线:与曲线交于两点,则或3、中点弦问题的方法:①方程组法,②代点作差法。两种方法总体都体现设而不求的数学思想。双曲线项目内容第一定义平面内与两个定点的距离之差等于常数(小于)的点的轨迹叫双曲线。第二定义平面内到定点与到定直线的距离之比为常数的点的轨迹叫双曲线。图形标准方程范围顶点与实虚轴的长焦点焦距准线方程焦半径当在右支上时左当在左支上时左当在上支上时下当在下支上时下渐近线方程焦准距离心率(越小,双曲线开口越小),等轴双曲线的准线间距对称性双曲线都是关于轴成轴对称,关于原点成中心对称通径第2页共3页焦点三角形双曲线上一点与双曲线的两个焦点组成的三角形,解题中常用余弦定理和勾股定理来进行相关的计算.焦点弦三角形双曲线的一焦点与过另一焦点的弦组成的三角形。参数方程为参数)为参数)(8)给出,等于已知是的平分线/(9)在平行四边形中,给出,等于已知是菱形;(10)在平行四边形中,给出,等于已知是矩形;(11)在中,给出,等于已知是的外心(三角形外接圆的圆心,三角形的外心是三角形三边垂直平分线的交点);(12)在中,给出,等于已知是的重心(三角形的重心是三角形三条中线的交点);(13)在中,给出,等于已知是的垂心(三角形的垂心是三角形三条高的交点);(14)在中,给出等于已知通过的内心;(15)在中,给出等于已知是的内心(三角形内切圆的圆心,三角形的内心是三角形三条角平分线的交点);(16)在中,给出,等于已知是中边的中线;五.了解下列结论(1)双曲线的渐近线方程为;(2)以为渐近线(即与双曲线共渐近线)的双曲线方程为为参数,≠0)。(3)中心在原点,坐标轴为对称轴的椭圆、双曲线方程可设为;第3页共3页项目内容定义平面内到定点的距离等于到定直线距离的点的轨迹叫抛物线。图形标准方程几何性质范围开口方向向右向左向上向下焦准距顶点坐标坐标原点(0,0)焦点坐标准线方程对称轴轴轴轴轴离心率通径长焦半径