分式加减（三）异分母的分式加减法VIP免费

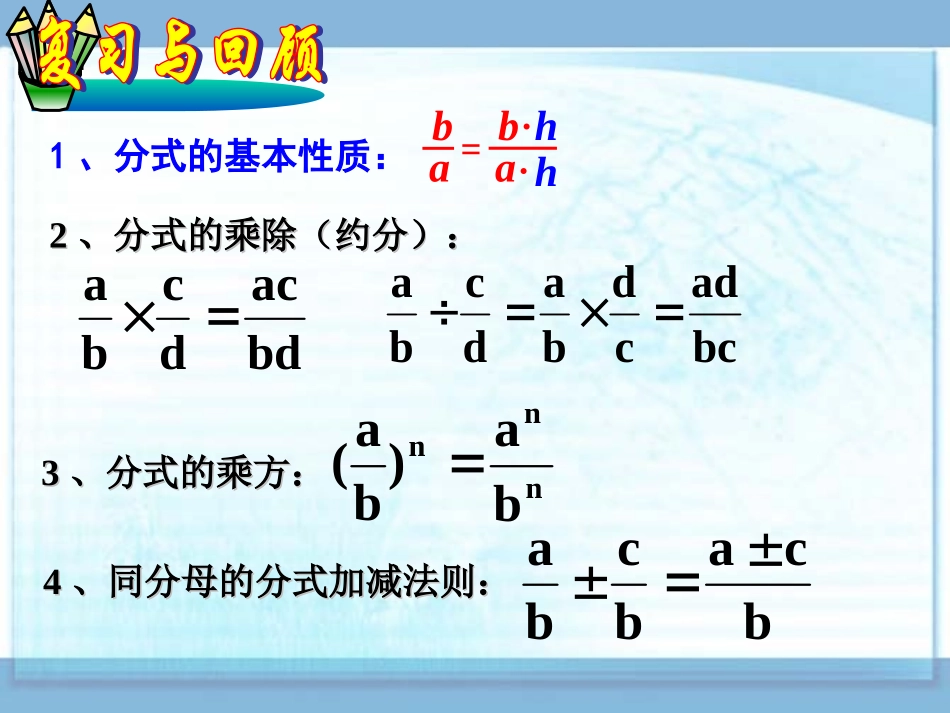
本节内容1.4（三）1、分式的基本性质：22、分式的乘除（约分）：、分式的乘除（约分）：bdacdcbabcadcdbadcba44、同分母的分式加减法则：、同分母的分式加减法则：33、分式的乘方：、分式的乘方：nnnba)ba(bcabcbaab=ab..hha15a12a3）1（xyxyxxyxyx）3（22xyyyxx）4（0a151232xyxy2yxyx2)a-12a+1+1-aa-3-a-15=a-12a+1-a+3-5=1小玲的妈妈买了一块蛋糕，分给小玲的弟弟这块蛋糕的，分给小玲这块蛋糕的，应当怎样切这块蛋糕？在图中画出来．1213·120°小玲和她的弟弟共分得这块蛋糕的几分之几？11121323532322366从上面的例子看到，异分母的分数相加，要先通分，化成同分母的分数，再加减。P27动脑筋v13v2+3v2+3v3=3v5=类似地，异分母的分式相加减，要先通分，即把各个分式的分子与分母都乘以适当的同一个非零多项式，化成同分母的分式，然后再加减．计算：注意：先确定公分母(各个分式的分母变成相同)，通分后，再计算。上述两例的公分母是？1x+11x-1-(1)1x+11x-1-解：x-1(x+1)(x-1)-=x+1(x+1)(x-1)(x-1)-(x+1)(x+1)(x-1)=-2x2-1=2x2-1=-3333xxxx(2)解：原式=(x-3)(x+3)(x+3)2(x-3)(x+3)(x-3)2-x2-9(x+3)2-(x-3)2=x2-912x=解：原式=222(2)()abababab112abab2(2)()(2)()abababababab2(2)()abababab2232baabb因式分解先化简，再确定最简公分母通分整式加减法则最简分式a2-4ab+4b2a-2ba2+2ab+b2a+b-(3)(4)x+1+1-x1解：x+1+1-x1=x+11+1-x1=(x+1)(1-x)1-x+1-x11-x1-x2+1=1-x2-x2=注意：计算时，先将分式化简再通分。整式与分式相加减，把整式看作为分母是“1”的分式。1、填空a24a1-(1)=a1b1+(2)=2、计算(3)xz12yx+=(4)4a2b2ac-=(2)2x4xx111++(3)x+2x-2x-2x+2(1)76x2y23xy223x(4)x-y2(x-y)53(5)x-y(x-y)2+a2-b2ab-b2(6)abab-a2-a24-aaba+b2xyz2y+x2z4a2b2-4ac6x2y27y-4x4x7x2-48x2x-2y4-3x(x-y)25x-5y+3ab2b2-a21、计算(2)12x-63x2-9(3)2aa2-41a-2(1)12m2-923-m(4)4x2-42x+2+1x-2(5)x-2-x+2x2(6)a+2-2-a4(7)-1-x1-x1x+2Ax-2B+=x2-43x-42、已知，求A，B的值。a1b1+=52a-2b+7aba-2ab-b3、已知，求的值。9小结：（1）分式加减运算的方法思路：通分转化为异分母相加减同分母相加减分子（整式）相加减分母不变转化为（2）分子相加减时，如果分子是一个多项式，要将分子看成一个整体，先用括号括起来，再运算，可减少出现符号错误。(3)分式加减运算的结果要约分，化为最简分式(或整式）。本节课你的收获是什么？作业：p29练习p30A3、4