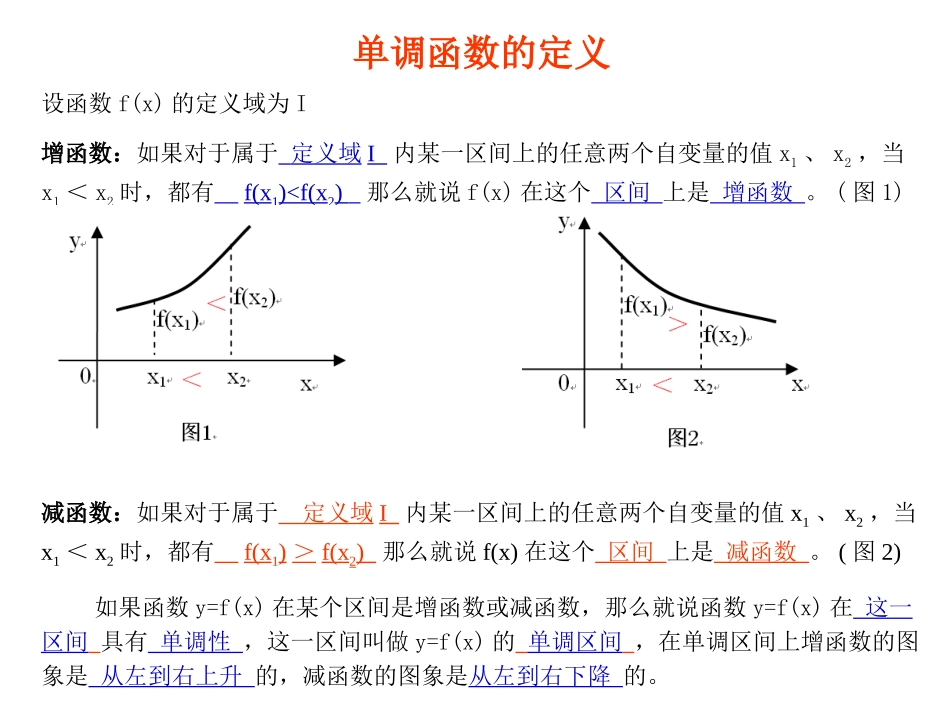
函数单调性(复习课)襄州一中刘双双单调函数的定义设函数f(x)的定义域为I增函数:如果对于属于定义域I内某一区间上的任意两个自变量的值x1、x2,当x1<x2时,都有f(x1)0)和单调具有一致性1()yfx3.导数法设函数f(x)在[ab]上连续在(a,b)内可导(1)如果在(ab)内f(x)>0则f(x)在[ab]上单调增加(2)如果在(ab)内f(x)<0则f(x)在[ab]上单调减少4.图象法5.复合函数单调性的判断:复合函数复合函数ff[[g(x)g(x)]]的单调性与构成的单调性与构成它的函数它的函数u=g(x)u=g(x),,y=f(u)y=f(u)的单调性密切相关,其规律如下:的单调性密切相关,其规律如下:函数函数单调性单调性u=g(x)u=g(x)增增增增减减减减y=f(u)y=f(u)增增减减增增减减y=fy=f[[g(x)g(x)]]增增减减减减增增例2。求下列函数的单调区间答案:(-∞,-3]单调减区间[2,+∞)单调增区间注意:求单调区间时,一定要先看定义域。21()6fxxx利用图象法求单调区间的时候,应特别注意某些特殊点,尤其是图象发生转弯的地方。用它们将定义域进行划分,再分别考察。2223yxxy=f(x)(f(x)恒不为0),与的单调性单调性相反。)(1xfy例3.判断函数xxxy4)2(22在(1,+∞)上的单调性。)上为减函数。在递减,故原函数)+(为正数且增函数,时,而当(解:,1(4244)2(1,4)241222xxuxxy1。求参数范围例1:已知函数y=x2-2ax+a2-1在(-∞,1)上是减函数,求a的取值范围。1],a)1],1222aaaaxxy即,(-,显然,(-,的减区间是(-解:解此类由二次函数单调性求参数范围的题,最好将二次函数的图象画出来,通过图象进行分析,可以将抽象的问题形象化。函数单调性应用22.,()log()2,4?aafxaxx例是否存在实数使函数在区间上是增函数22244202441640aaxxaaaaaxxaaa解:当>1时,则只需函数u=在区间,上为1增且为正,即2且,解得>12当01时,则只需函数u=在区间,上为1减且为正,即且,无解2函数单调性应用本题主要是考查复合函数的单调性,当内外函数的增本题主要是考查复合函数的单调性,当内外函数的增减性一致时,为增函数;当内外函数的增减性相异时,为减减性一致时,为增函数;当内外函数的增减性相异时,为减函数函数..另外,复合函数的单调区间一定是定义域的子区间,另外,复合函数的单调区间一定是定义域的子区间,在解题时,要注意这一点在解题时,要注意这一点..所以,存在实数a,且a>12...