三角函数的图像和性质()VIP免费

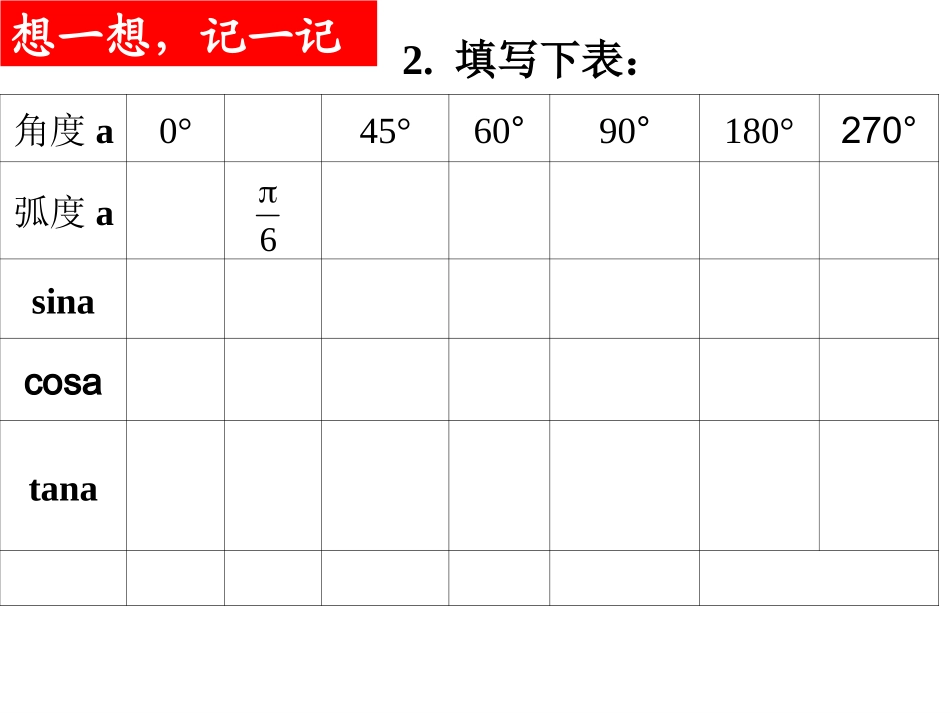
1.4.２正弦.余弦函数的性质(2)任意角三角函数的定义定义单位圆中一般地图象sincostanOP(x,y)xyA(1,0)αOxyP(x,y)y||(0)OPrryrxxryxyx温故知新。。2.填写下表：角度a0°45°60°90°180°270°弧度asinacosatana6想一想，记一记x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同正弦和余弦函数的图像(1)今天是星期一，则过了七天是星期几?过了十四天呢？……(2)物理中的单摆振动，表针的运动规律如何呢？问题与思考(1)正弦函数的图象是有规律不断重复出现的；(2)规律是：每隔2重复出现一次（或者说每隔2k，kZ重复出现）；(3)这个规律由诱导公式sin(2k+x)=sinx可以说明.正弦函数的性质1——周期性结论：象这样一种函数叫做周期函数.观察与思考对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有：f(x＋T)＝f(x).那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.周期函数定义：思考辨析例1求下列函数的周期：（1）y=3cosx;x∈R（2）y=sin2x，x∈R；1(3)2sin(),26yxxR学以致用由以上几例你认为三角函数的周期与解析式中的哪些量有关呢？1sin3123sin24yxxRyxxR课堂练习：求下列函数的周期（），（）（），学以致用一般结论:归纳总结正弦、余弦函数的性质2——奇偶性请同学们观察正、余弦函数的图形，说出函数图象有怎样的对称性？其特点是什么？y＝cosxy＝sinx观察与思考1.正弦函数、余弦函数的周期性；2.正弦函数、余弦函数的奇偶性；3.正弦函数、余弦函数的性质还有哪些呢？课堂小结再见！课本P４６１，３