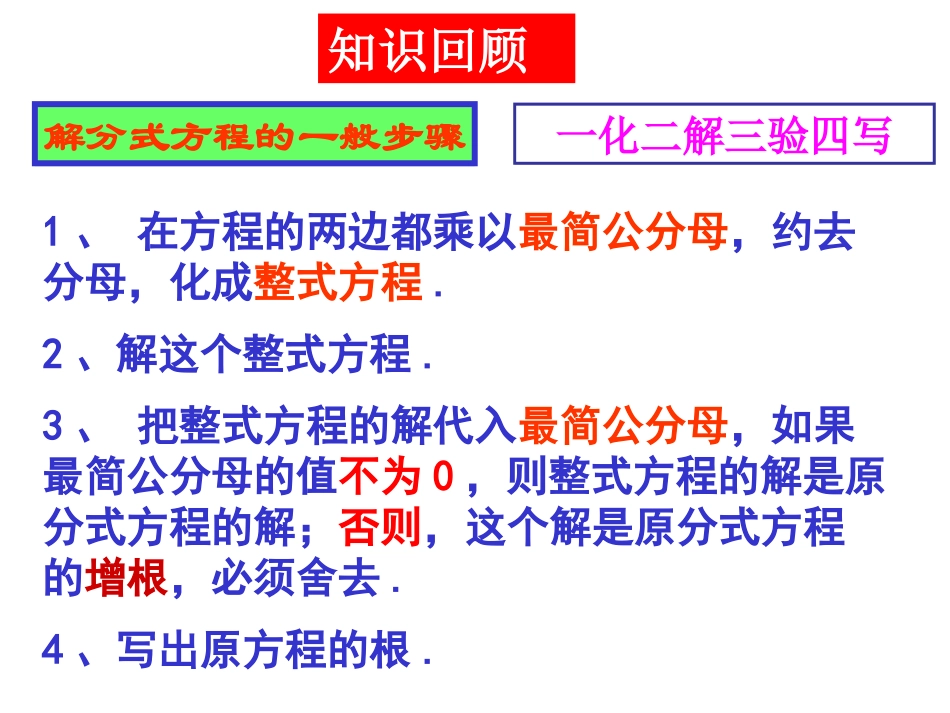
解分式方程的一般步骤1、在方程的两边都乘以最简公分母,约去分母,化成整式方程.2、解这个整式方程.3、把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解是原分式方程的增根,必须舍去.4、写出原方程的根.一化二解三验四写知识回顾123111xxxx、解方程._______31322的值等于增根,则有的分式方程、若关于mxmxx3、已知关于x的方程无解,求a的值。基本上有4种:(3)行程问题:路程=速度×时间以及它的两个变式;(1)和差倍分问题:寻找关键词“比多、比少、相等、增加、减少等”(2)工程问题:工作量=工时×工效以及它的两个变式;(4)利润问题:进价,标价,售价,利润,利润率等概念;常见的几种题型列分式方程解应用题的基本步骤是:(1)审——审清题意、找等量关系.(2)设——设未知数.(3)列——根据等量关系列方程.(4)解——解方程.(5)验——既要验是否为所列分式方程的根,又要验是否符合实际情况(6)答——写出答案.例1.某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:同学们,请求出篮球和排球的单价各是多少元?1、和差倍分问题几个小伙伴打算去音乐厅看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:根据对话中的信息,请你求出这些小伙伴的人数.教材P36:A组T32、工程问题例2两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?练1、抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?练2、书本P36练习T1例3、某校八年级学生乘车前往某景点秋游,现有两条线路可供选择:线路一全程25km,线路二全程30km;若走线路二平均车速是走线路一的1.5倍,所花时间比走线路一少用10min,则走线路一、二的平均车速分别为多少?3、行程问题1、李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校,已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)李明步行的速度是多少千米/小时?(2)李明能否在联欢会开始前赶到学校?2、船航行于相距32千米的两码头之间,逆水比顺水多用了12小时,若水流速度比船在静水中的速度少2千米/时,求水流速度及船在静水中速度.练3、书本P36练习T24、利润问题例4:教材P35例3练1、某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完。(1)该种干果的第一次进价是每千克多少钱?(2)超市销售这种干果共盈利多少元?练2:“母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着有用了5000元购进第二批这种盒装花,已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元,求第一批盒装花每盒的进价是多少元?练2、P37T7.练4、某果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完;由于水果畅销,第二次购买时,每千克的进价比第一次提高10,用1452元所购买的数量比第一次多20千克,因出现高温天气,水果不易保鲜,为减少损失,便降价50售完剩余的水果。(1)求第一次水果的进价是每千克多少元?(2)该果品店在这两次销售中,总体是盈利还是亏损?盈利或亏损了多少元?