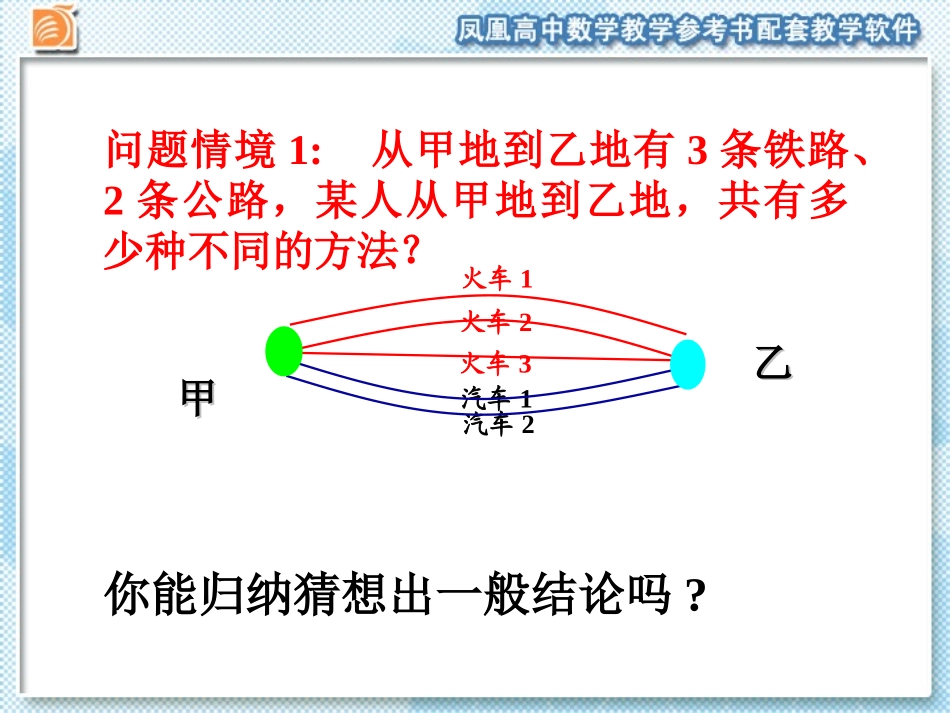
问题情境1:从甲地到乙地有3条铁路、2条公路,某人从甲地到乙地,共有多少种不同的方法?火车2火车1火车3汽车1汽车2乙乙甲甲你能归纳猜想出一般结论吗?问题情境2:某人欲自A地经B地到C地,从A地到B地一天中有火车3班,从B地到C地有汽车2班,那么从A地到C地有多少种不同的走法?火车1汽车1火车2火车3汽车2ABC某人欲自A地经B地到C地,从A地到B地一天中有火车3班,从B地到C地有汽车2班,那么从A地到C地有多少种不同的走法?问题情境2你能归纳猜想出一般结论吗?ABC知识建构分类计数原理:(从例1可以看出)完成一件事情,有有nn类方式类方式,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,……在第n类方式中有mn种不同的方法.那么完成这件事共有N=种不同的方法.两个基本计数原理.mm11++mm22+…++…+mmnn知识建构分步计数原理:(从例2可以看出)完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……做第n步有mn种不同的方法.那么完成这件事共有N=种不同的方法.两个基本计数原理.mm11××mm22×…××…×mmnn数学运用例1某班共有男生28名、女生20名,从该班选出学生代表参加校学代会.(1)若学校分配给该班1名代表,则有多少种不同的选法?(2)若学校分配给该班2名代表,且男、女代表各1名,则有多少种不同的选法?例2(1)在图(1)的电路中,只合上一只开关以接通电路,有多少种不同的方法?(2)在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?数学运用例3为了确保电子信箱的安全,在注册时,通常要设置电子信箱密码,在某网站设置的信箱中,(1)密码为4位,每位均为0到9这10个数字中的一个,这样的密码共有多少个?(2)密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的一个.这样的密码共有多少个?(3)密码为4~6位,每位均为0到9这10个数字中的一个.这样的密码共有多少个?数学运用例4有5种不同的书(每种不少于3本),从中选购3本送给3名同学,每人各1本,共有多少种不同的送法.数学运用练习:练习.(1)现有高一年级的学生4名,高二年级的学生5名,高三年级的学生3名.(2)若4名学生报名参加数学、计算机、航模兴趣小组,每人选报1项,则有多少种报名方法?①从中任选一人参加夏令营,有种不同的选法?②从每个年级的学生中各选一人参加夏令营,有多少种不同的选法?课堂小结弄清两个原理的区别与联系,是正确使用这两个原理的前提和条件.这两个原理都是指完成一件事,区别在于:(1)分类(加法)计数原理是“分类”,每类办法中的每一种方法都能独立独立完成一件事;(2)分步(乘法)计数原理是“分步”;每种方法都只能做这件事的一步,不能独立完成这件事,只有各个步骤都完成才算完成这件事情!