一元二次方程根的判别式VIP免费

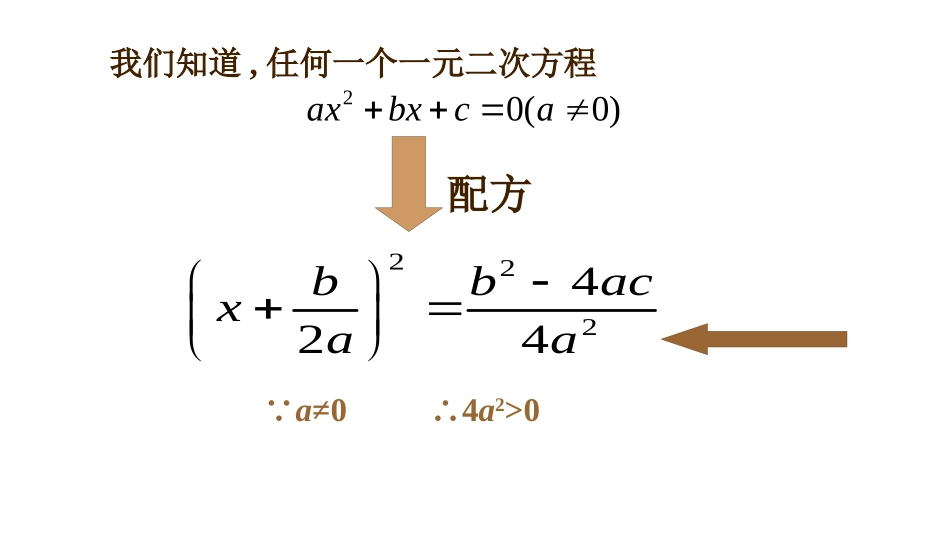
2.3一元二次方程根的判别式我们在运用公式法解一元二次方程ax2+bx+c=0（a≠0）时，总是要求b2-4ac≥0.这是为什么？.0223;0122;02121222xxxxxx）（）（）（用公式法解下列方程：我们知道,任何一个一元二次方程)0(02acbxax∵a≠0222424bbacxaa∴4a2>0配方∵a≠04∴a2>0222424bbacxaa当时，240bac当时，240bac当时，240bac221244,.22bbacbbacxxaa方程有两个不相等的实数根：12.2bxxa方程有两个相等的实数根：方程没有实数根.1.3.2.我们把叫做一元二次方程的根的判别式，用符号“”表示，即.24bac200axbxca24bac结论1.当时，方程有两个不相等的实数根，其根为：0一元二次方程：的根的情况可由来判断：200axbxca24bac2.当时，方程有两个相等的实数根，其根为：=03.当时，方程有没有实数根.0x1=，x2=；aacbb242aacbb242x1=x2=；ab2例题讲解例不解方程，利用判别式判断下列方程根的情况.（1）3x2－x＋1=3x；（2）5（x2＋1）=7x；（3）x2－4x=－4.方程要先化为一般形式，再求判别式（1）今天我们学习了根的判别式的应用（2）注意根的判别式定理与逆定理的使用区别：当已知△值的符号时，使用定理；当已知方程根的情况时，使用逆定理。)(221xxab)(2021xxab判别式情况根的情况定理与逆定理△＞0X1,X2=≥△0<=>有（两个）实数根△＞0<=>有两个不等实数根△＝0X1,X2=△=0<=>有两个相等实数根△＜0无意义,X1,X2不存在△＜0<=>无实根1.一元二次方程x2+2x+4=0的根的情况是（）A.有一个实数根B.有两个相等的实数根C.有两个不相等的实数根D.没有实数根D2.方程x2-3x+1=0的根的情况是（）A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.只有一个实数根A3.下列一元一次方程中，有实数根的是（）A.x2-x+1=0B.x2-2x+3=0C.x2+x-1=0D.x2+4=0C练习4.不解方程，利用判别式判别下列方程的根的情况：（3）2y2-3y+4=0；（4）（1）x2+3x-1=0；（2）x2-6x+9=0；2+5=25xx.练习5.若方程2x2-(k-1)x+8=0有两个相等的实数根，求k的值.解：.8),1(,2ckba82412)]([k.6322kk又∵方程有两个相等的实数根,.0632,02kk即.79kk或