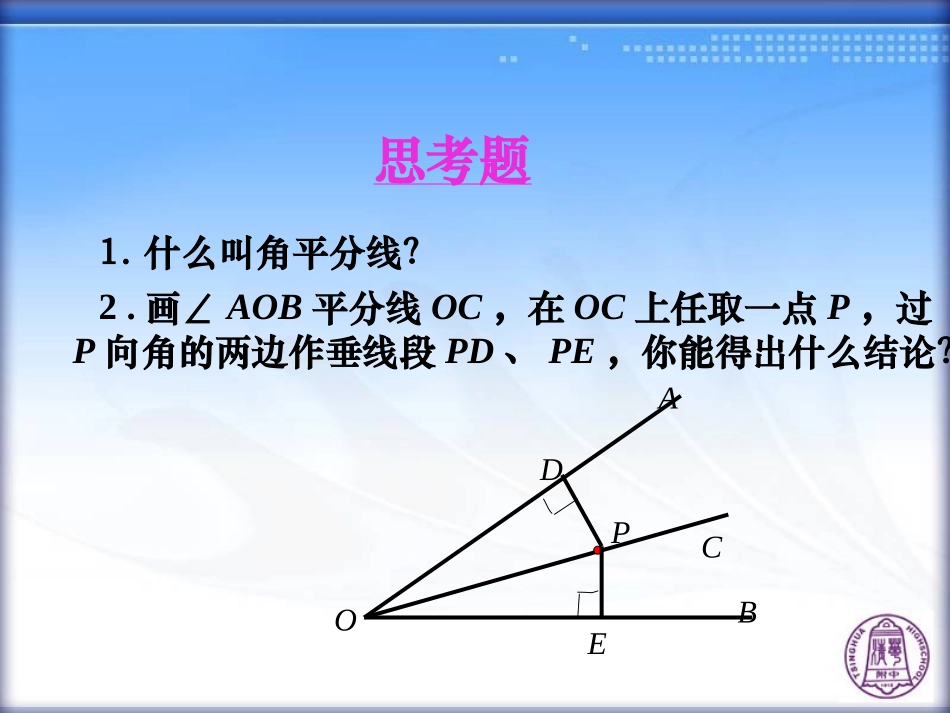
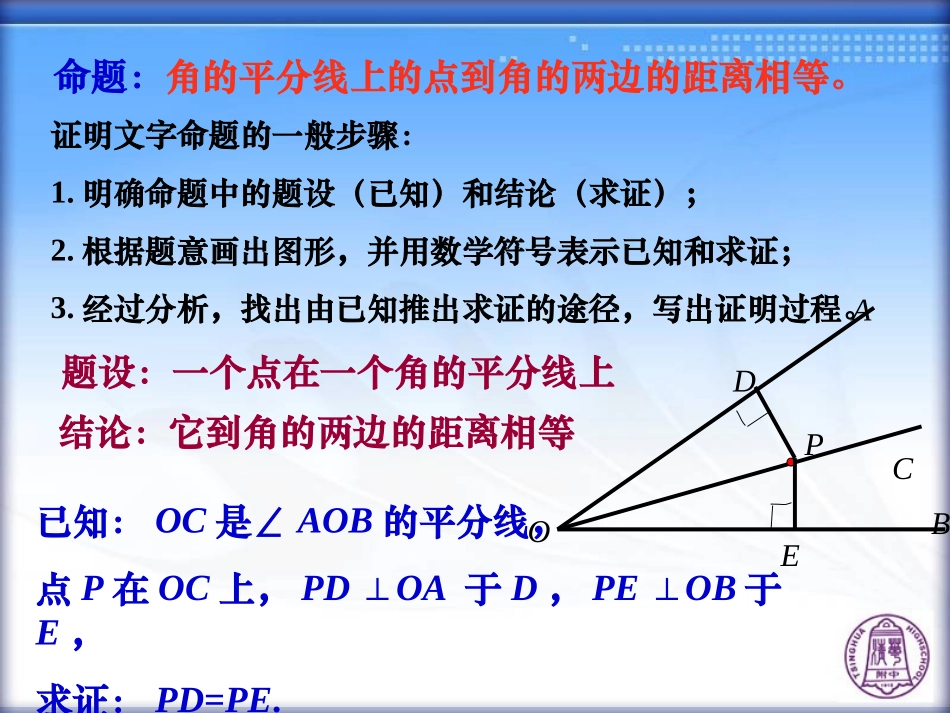
11.3角平分线的性质与判定1.什么叫角平分线?2.画∠AOB平分线OC,在OC上任取一点P,过P向角的两边作垂线段PD、PE,你能得出什么结论?思考题AOBPEDC命题:角的平分线上的点到角的两边的距离相等。题设:一个点在一个角的平分线上结论:它到角的两边的距离相等已知:OC是∠AOB的平分线,点P在OC上,PD⊥OA于D,PE⊥OB于E,求证:PD=PE.证明文字命题的一般步骤:1.明确命题中的题设(已知)和结论(求证);2.根据题意画出图形,并用数学符号表示已知和求证;3.经过分析,找出由已知推出求证的途径,写出证明过程。AOBPEDC∵∠1=2∠PD⊥OA,PE⊥OB∴PD=PE.角平分线的性质定理角的平分线上的点到角的两边的距离相等。用符号语言表示为:AOBPED12交换定理的题设和结论得到的命题为:C角的内部到角的两边的距离相等的点在角的平分线上。已知:PD⊥OA于D,PE⊥OB于E,PD=PE.求证:点P在∠AOB的平分线上。角平分线的判定定理AOBPDEC用符号语言表示为:∵PD=PEPD⊥OA,PE⊥OB∴∠1=2.∠12练一练填空:(1).1=2∵∠∠,DC⊥AC,DE⊥AB∴___________(___________________________________________)(2).∵DC⊥AC,DE⊥AB,DC=DE∴__________(______________________________________________)ACDEB12∠1=2∠DC=DE角的内部到角的两边的距离相等的点在角的平分线上角的平分线上的点到角的两边的距离相等例1已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F,求证:EB=FC。BAEDCF例2如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且BE=CF。求证:AD是△ABC的角平分线。ABCEFD例3如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF,求证:CF=EB。FEDCBA例4如图,已知:BD⊥AM于点D,CE⊥AN于点E,BD、CE交点F,CF=BF,求证:点F在∠A的平分线上.ADNEBFMCA例5如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等。∵点P在△ABC的角平分线BM上,PE⊥BC,PD⊥ABABCPMNDEF(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PE=PF.即点P到三边AB、BC、CA的距离相等证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F∴PD=PEP练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.ABCDEFGHMN例6如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠BAC的平分线上.证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于MGHM∵点F在∠BCE的平分线上,FG⊥AE,FM⊥BC∴FG=FM同理可证FM=FH∴FG=FH∴点F在∠DAE的平分线上又∵FG⊥AE,FH⊥AD利用结论,解决问题练一练1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?想一想在确定度假村的位置时,一定要画出三个角的平分线吗?你是怎样思考的?你是如何证明的?拓展与延伸2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处B.两处C.三处D.四处分析:由于没有限制在何处选址,故要求的地址共有四处。D课堂小结1.角平分线的性质定理:角的平分线上的点到角的两边的距离相等。2.角平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上。3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径.