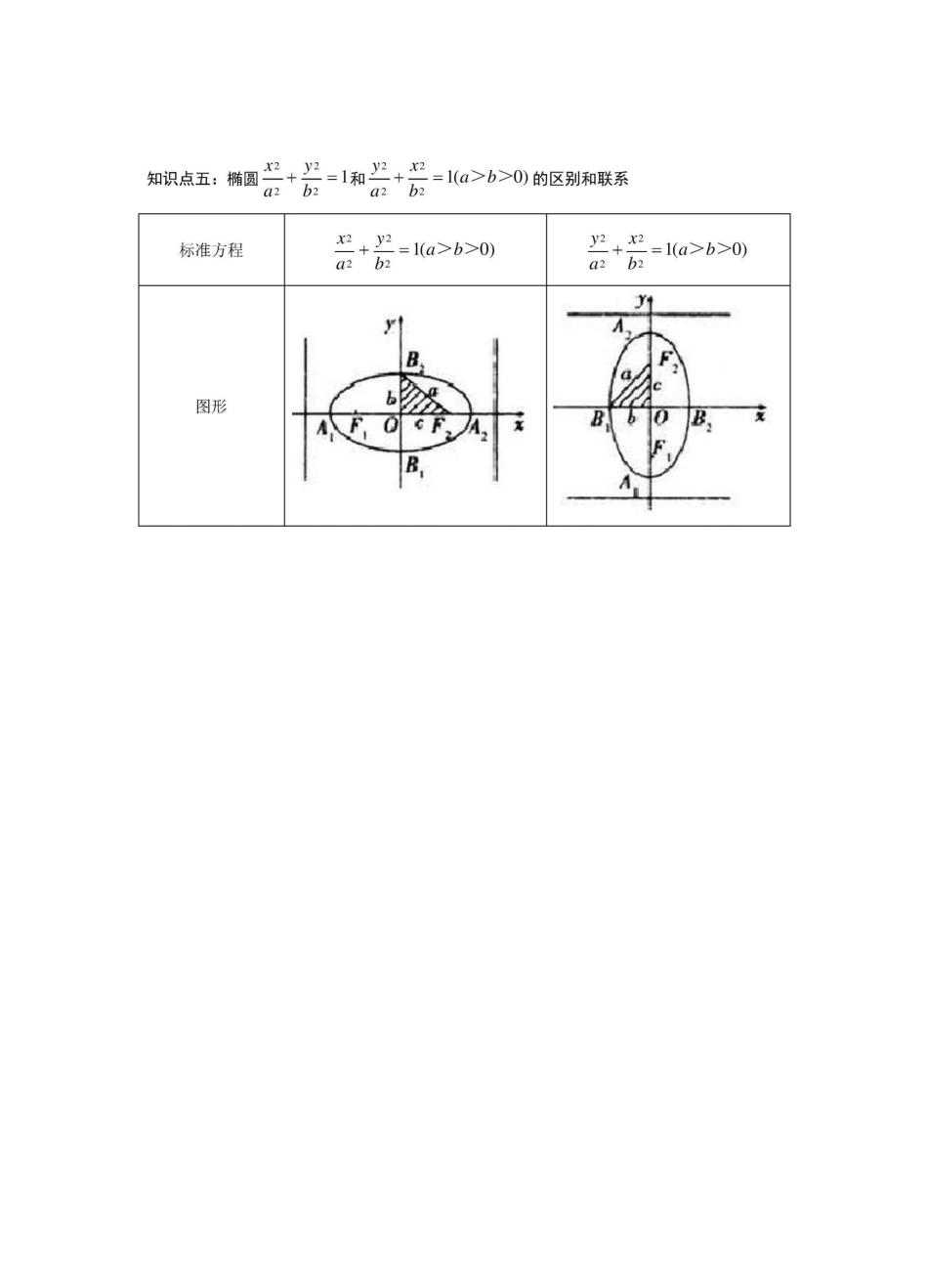
1、当焦点在x轴上时,椭圆的标准方程,其中c2=a2一b2、当焦点在y轴上时,椭圆的标准方程,其中c2=a2一b椭圆的基本知识一、基本知识点知识点一:椭圆的定义:椭圆三定义,简称和比积1、定义1:(和)到两定点的距离之和为定值的点的轨迹叫做椭圆。这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距,定值为。2、定义2:(比)到定点和定直线的距离之比是定值的点的轨迹叫做椭圆。定点为焦点,定直线为准线,定值为。3、定义3:(积)到两定点连线的斜率之积为定值的点的轨迹是椭圆。两定点是长轴端点,定值为m=e2-1(—lVmVO)。知识点二:椭圆的标准方程知识点三:椭圆的参数方程x2y2+=1(a>b>0)的参数方程为a2b2知识点四:椭圆的一些重要性质(1)对称性:椭圆的标准方程是以x轴、y轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心就是椭圆的中心。(2)范围:椭圆上所有的点都位于直线x=±a和y=±b所围成的矩形内,所以椭圆上点的坐标满足|x|
b>°)与坐标轴的四个顶点分别为•③椭圆的长轴和短轴。(4)离心率:①椭圆的焦距与长轴长度的比叫做椭圆的离心率,用e表示,记作e=2-=-2aa②因为a>c>0,所以e的取值范围是OVeVl。⑸焦半径:椭圆上任一点P(Xo,yo)到焦点的连线段叫做焦半径。对于焦点在兀轴上的椭圆,左焦半径[=a+exo,右焦半径[=a-eXo。a2(6)准线方程:x=±-cb2(7)焦准距:焦点到准线的距离,用p表示,记作p=-c仍为椭圆。(8)通径:过焦点垂直于长轴的直线与椭圆的两交点之间的距离称为椭圆的通径,长用dcb22b2表示,记作d—2ep—2.—.—aca(9)切线方程:过椭圆—+二—l(a>b>0)上(x,y)点的切线方程,可以用(x,y)等a2b2ooooxxyy效代替椭圆方程得到。等效代替后的切线方程是:i+0—1。a2b2(10)极点与极线:若P(x,y)是椭圆—+二—1(a>b>0)外一点,过P作椭圆的两000a2b20条切线,切点为P,P,则点P和切点弦PP分别称为椭圆的极点和极线。12012切点弦PP的直线方程即极线方程是+字—1(极线定理)。12a2b2(11)中点弦方程和弦中点轨迹:中点弦AB的方程:在椭圆中,若弦AB的中点为M(x,y),弦AB称为中点弦,则中点00xxyyx2y2弦的方程就是一+0——0+亠,是直线方程。a2b2a2b2弦中点M的轨迹方程:在椭圆中,过椭圆内点P(x,y)的弦AB,其中点M的方程就是000xxyyx2y2—0+——+-a2b2a2b2性质焦占八\、焦距范围对称性顶点轴长离心率准线方程焦半径二、规律方法1、如何确定椭圆的标准方程?确定一个椭圆的标准方程需要三个条件:两个定形条件a,b;一个定位条件焦点坐标,由焦点坐标的形式确定标准方程的类型。2、椭圆标准方程中的三个量a,b,c的几何意义a,b,c构成一个直角三角形的三边,满足勾股定理。3、如何由椭圆标准方程判断焦点的位置?椭圆的焦点总在长轴上,因此已知标准方程,判断焦点位置的方法是:看x2,y2的分母的大小,哪个分母大,焦点就在哪个坐标轴上。4、方程Ax2+By2二C(ABC丰0)是表示椭圆的条件。5、求椭圆标准方程的常用方法:①待定系数法:由已知条件确定焦点的位置,从而确定椭圆方程的类型,设出标准方程,再由条件确定方程中的参数a,b,c的值。其主要步骤是“先定型,再定量”②定义法:由已知条件判断出动点的轨迹是什么图形,然后再根据定义确定方程。6、共焦点的椭圆标准方程形式上的差异x2y2共焦点,则c相同。与椭圆一+1二l(a>b>0)共焦点的椭圆方程可设为a2b2x2y2+二1(m>-b2),此类问题常用待定系数法求解。a2+mb2+m7、如何求解与焦三角形APF1F(P是椭圆上的点)有关的计算问题?焦三角形:以椭圆的两个焦点F,F为顶点,另一个顶点P在椭圆上的三角形称为焦三角形。12g半角是指g=ZFPF的一半。则焦三角形的面积为:S=b2tan。1228、直线与椭圆问题的有关计算问题(韦达定理的应用)(1)弦长公式(2)中点弦问题(点差法)三、四种题型与三种方法(一)四种题型x2y21、已知椭圆C:+=1内有一点A(2,l),F为椭圆C的左焦点,P为椭圆C上的一动2516点,求|PA+5|PF|的最小值。x2y22、已知椭圆C:25+话=1内有一点A(2J),卩为椭圆C的左焦点,P为椭圆C上的一动点,求|PA|+|PF|的最大...