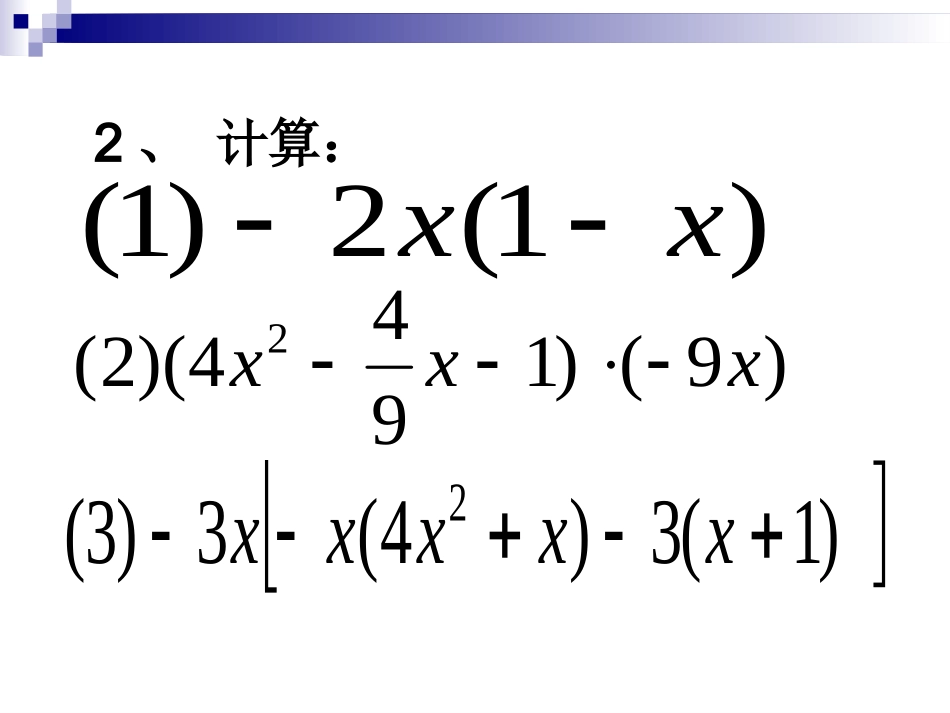多项式与多项式相乘VIP免费

回顾与思考回顾回顾&&思考思考☞☞②②再把所得的积相加再把所得的积相加。。如何进行如何进行单项式与多项式乘法的单项式与多项式乘法的运算？运算？①①将将单项式分别乘以多项式的各项，单项式分别乘以多项式的各项，进行进行单项式与多项式乘法单项式与多项式乘法运算时，要注意什么运算时，要注意什么??①①不能漏乘不能漏乘::即单项式要乘遍多项式的每一项即单项式要乘遍多项式的每一项②②去括号时注意符号的确定去括号时注意符号的确定..2、计算：)1(2)1(xx)9()1944)(2(2xxx)1(3)4(3)3(2xxxxx以下有四种不同形状的长方形以下有四种不同形状的长方形卡片，请你选取其中的两张，卡片，请你选取其中的两张，用它们拼成更大的长方形，尽用它们拼成更大的长方形，尽可能采用多种拼法。可能采用多种拼法。aammnnbbaabbmmnn（1）（2）（3）（4）aammnnaabbnnaammaabbnnbbmmnnm(a+n)=ma+mnm(a+n)=ma+mnb(a+n)=ba+bnb(a+n)=ba+bnn(m+b)=mn+bnn(m+b)=mn+bna(m+b)=am+aba(m+b)=am+abaammnnbbnn=ma+mn+ba+bn=ma+mn+ba+bn((转化为单项式乘以单项式转化为单项式乘以单项式))从代数运算的角度验证：从代数运算的角度验证：(m+b)(a+n)(m+b)(a+n)=m(a+n)+b(a+n)=m(a+n)+b(a+n)（把（把a+na+n看作一个整体）看作一个整体）多项式与多项式相乘，先用一个多项多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的式的每一项分别乘以另一个多项式的每一项，再把所得的积相加每一项，再把所得的积相加多项式与多项式相乘的法则多项式与多项式相乘的法则在进行多项式乘法运算的推导过在进行多项式乘法运算的推导过程中运用了哪些数学思想方法？与同伴程中运用了哪些数学思想方法？与同伴交流。交流。运用了整体、转化和数形结合的数学思想运用了整体、转化和数形结合的数学思想。。例题解析【【例例11】】计算：计算：(1)(1)(x+2)(x(x+2)(x−−33)),,(2)(2)(3(3xx-1-1)(2)(2xx+1+1))。。解解::(1)(1)(x+2)(x(x+2)(x−−33))−−3x3xxx==xx22-x-6-x-6-2-2×3×3（（22））(3(3xx-1-1)(2)(2xx+1+1))====xx﹒﹒xx33xx••22xx++33xx••11-1-1••22xx−−11==66xx22+3+3xx-2-2xx−−11==66xx22++xx−−..所得积的符号由这所得积的符号由这两项的符号来确定：两项的符号来确定：负负负负得正得正一正一负一正一负得负。得负。注意注意两项两项相乘时，相乘时，先定符号。先定符号。☾☾最后的结最后的结果要合并同类项果要合并同类项..【【例例22】】计算：计算：(1)(x(1)(x−3y−3y)(x)(x+7y+7y),(2)(2),(2)(2xx++55yy)(3)(3xx−2−2yy))。。解解::(1)(1)(x−3y)(x+7y)(x−3y)(x+7y)7xy7xy−−3yx3yx--==xx22+4xy-21y+4xy-21y22；；21y21y22（（22））(2(2xx+5+5yy)(3)(3xx−2−2yy))====xx2222xx••33xx−−22xx••22yy+5+5yy••33xx−−5y5y••22yy==6x6x22−−44xyxy++15xy15xy−−yy22==6x6x22+11+11xyxy−−yy22..随堂练习随堂练习随堂练习(1)(1)((mm++22nn)()(mm−−22nn))；；(2)(2)(2(2nn++5)(5)(nn−−3)3);;㈠㈠计算：计算：(3)(3)((xx++22yy))22;;(4)(4)((axax++bb)()(cxcx++dd))..注意：1、必须做到不重复，不遗漏.2、注意确定积中每一项的符号.3、结果应化为最简式{{合并同类项合并同类项}}．．师生小结：比一比：(1)(x+5)(x–7)(2)(2a+3b)(2a+3b)(3)(x+5y)(x–7y)(4)(2m+3n)(2m–3n)【【例例33】】计算：计算：28231215aaaaa练一练：1、2、25xx+2x+1-2x+3x-53123＋3x-4xxx【【例例55】】：解方程与不等式：：解方程与不等式：22y-2y+2y+4-yy-2y-1,其中y=-1【【例例44】】化简求值：化简求值：21、2x+342362、3x+434923xxxxxxx挑战极限：如果(x2+bx+8)(x2–3x+c)的乘积中不含x2和x3的项，求b、c的值。解：原式...