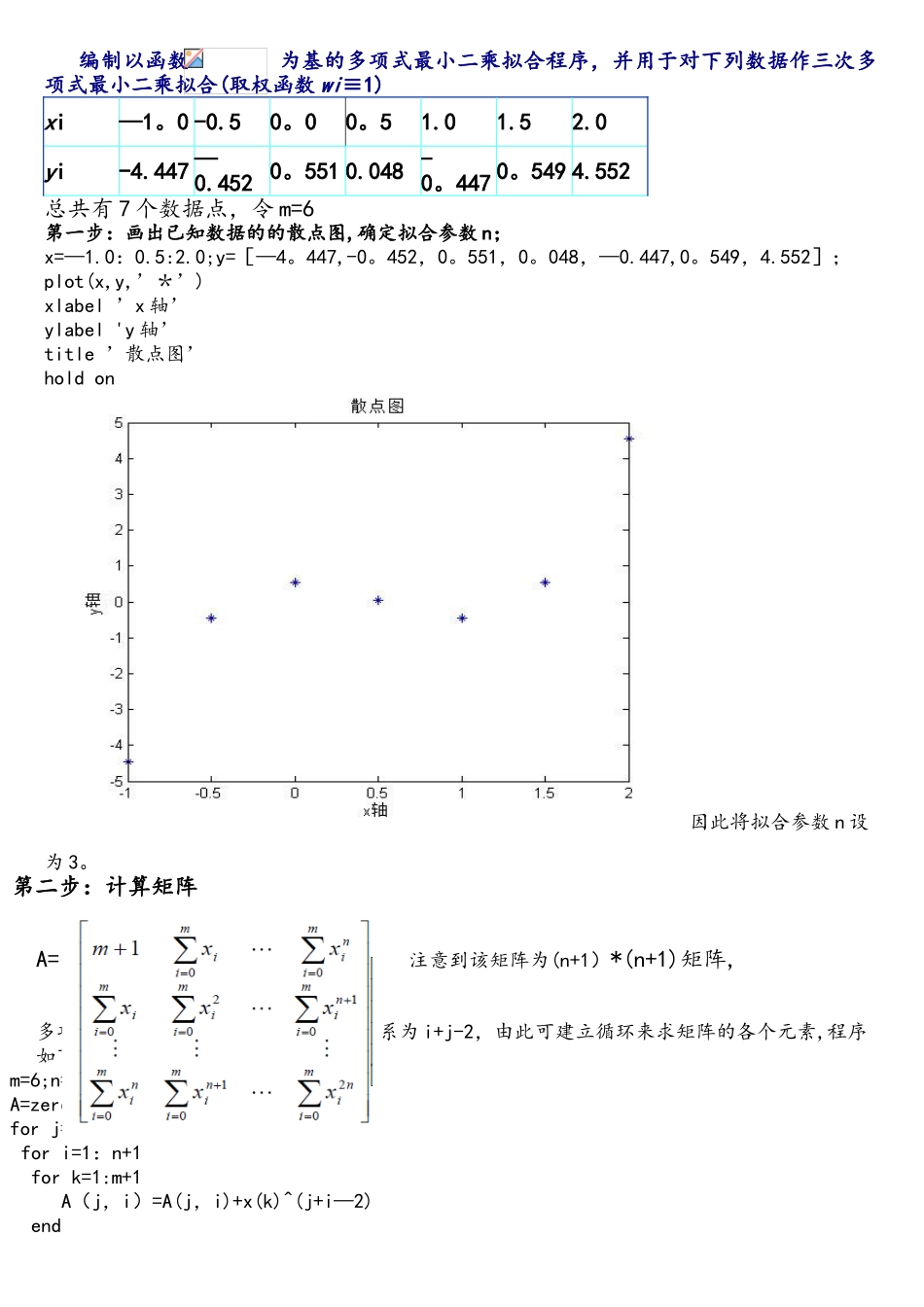
用最小二乘法进行多项式拟合(matlab 实现)西安交通大学 徐彬华算法分析:对给定数据 (i=0 ,1,2,3,。。,m),一共 m+1 个数据点,取多项式 P(x),使函数 P(x)称为拟合函数或最小二乘解,令似的 使得 其中,a0,a1,a2,…,an 为待求未知数,n 为多项式的最高次幂,由此,该问题化为求的极值问题。由多元函数求极值的必要条件: j=0,1,…,n得到: j=0,1,…,n这是一个关于 a0,a1,a2,…,an 的线性方程组,用矩阵表示如下:因此,只要给出数据点 及其个数 m,再给出所要拟合的参数 n,则即可求出未知数矩阵(a0,a1,a2,…,an)试验题 1编制以函数 为基的多项式最小二乘拟合程序,并用于对下列数据作三次多项式最小二乘拟合(取权函数 wi≡1)xi—1。0 -0.50。00。51.01.52.0yi-4.447 —0.452 0。551 0.048 -0。447 0。549 4.552总共有 7 个数据点,令 m=6第一步:画出已知数据的的散点图,确定拟合参数 n;x=—1.0:0.5:2.0;y=[—4。447,-0。452,0。551,0。048,—0.447,0。549,4.552];plot(x,y,’*’)xlabel ’x 轴’ylabel 'y 轴’title ’散点图’hold on因此将拟合参数 n 设为 3。第二步:计算矩阵A= 注意到该矩阵为(n+1)*(n+1)矩阵,多项式的幂跟行、列坐标(i,j)的关系为 i+j-2,由此可建立循环来求矩阵的各个元素,程序如下:m=6;n=3;A=zeros(n+1);for j=1:n+1 for i=1:n+1 for k=1:m+1 A(j,i)=A(j,i)+x(k)^(j+i—2) end endend;再来求矩阵B=B=[0 0 0 0];for j=1:n+1 for i=1:m+1 B(j)=B(j)+y(i)*x(i)^(j—1) endend第三步:写出正规方程,求出 a0,,a1…,an.B=B';a=inv(A)*B;第四步:画出拟合曲线x=[-1.0:0.0001:2。0];z=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3;plot(x,z) legend(’离散点’,’y=a(1)+a(2)*x+a(3)*x。^2+a(4)*x。^3')title('拟合图')总程序附下:x=-1。0:0.5:2.0;y=[-4。447,-0.452,0.551,0。048,—0.447,0。549,4。552];plot(x,y,’*’)xlabel 'x 轴'ylabel ’y 轴'title '散点图'hold onm=6;n=3;A=zeros(n+1);for j=1:n+1 for i=1:n+1 for k=1:m+1 A(j,i)=A(j,i)+x(k)^(j+i-2) end endend;B=[0 0 0 0];for j=1:n+1 for i=1:m+1 B(j)=B(j)+y(i)*x(i)^(j—1) endendB=B’;a=inv(A)*B;x=[—1.0:0.0001:2。0];z=a(1)+a(2)*x+a(3)*x.^2+a(4)*x。^3;plot(x,z) legend(’离散点’,’y=a(1)+a(2)*x+a(3)*x.^2+a(4)*x.^3')title(’拟合图’)