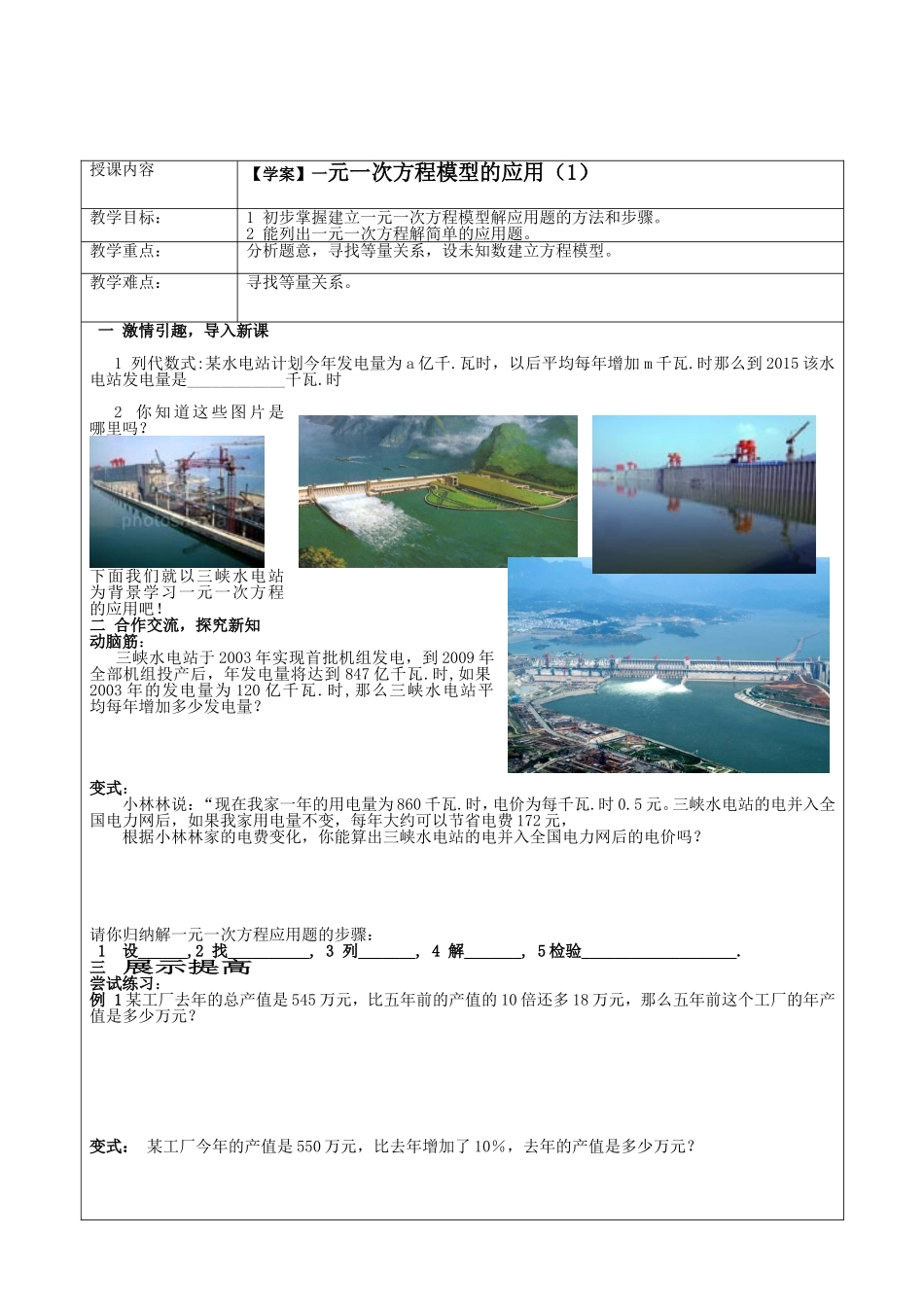
授课内容【学案】一元一次方程模型的应用(1)教学目标:1初步掌握建立一元一次方程模型解应用题的方法和步骤。2能列出一元一次方程解简单的应用题。教学重点:分析题意,寻找等量关系,设未知数建立方程模型。教学难点:寻找等量关系。一激情引趣,导入新课1列代数式:某水电站计划今年发电量为a亿千.瓦时,以后平均每年增加m千瓦.时那么到2015该水电站发电量是____________千瓦.时2你知道这些图片是哪里吗?下面我们就以三峡水电站为背景学习一元一次方程的应用吧!二合作交流,探究新知动脑筋:三峡水电站于2003年实现首批机组发电,到2009年全部机组投产后,年发电量将达到847亿千瓦.时,如果2003年的发电量为120亿千瓦.时,那么三峡水电站平均每年增加多少发电量?变式:小林林说:“现在我家一年的用电量为860千瓦.时,电价为每千瓦.时0.5元。三峡水电站的电并入全国电力网后,如果我家用电量不变,每年大约可以节省电费172元,根据小林林家的电费变化,你能算出三峡水电站的电并入全国电力网后的电价吗?请你归纳解一元一次方程应用题的步骤:1设______,2找__________,3列_______,4解_______,5检验___________________.三展示提高尝试练习:例1某工厂去年的总产值是545万元,比五年前的产值的10倍还多18万元,那么五年前这个工厂的年产值是多少万元?变式:某工厂今年的产值是550万元,比去年增加了10%,去年的产值是多少万元?(一)怎样调配劳动力?例2在甲处劳动的有27人,在乙处劳动的有19人,现在调20人去支援,使甲处人数是乙处人数的2倍,应调往甲、乙两处各多少人?变式:全班同学去划船,如果减少一条船,每条船正好坐10个同学,如果增加一条船,每条船正好坐好8个同学,问这个班有多少同学?四.反思小结,拓展提高解方程应用题的步骤是什么?要注意些什么?五作业