第3章实数复习VIP免费

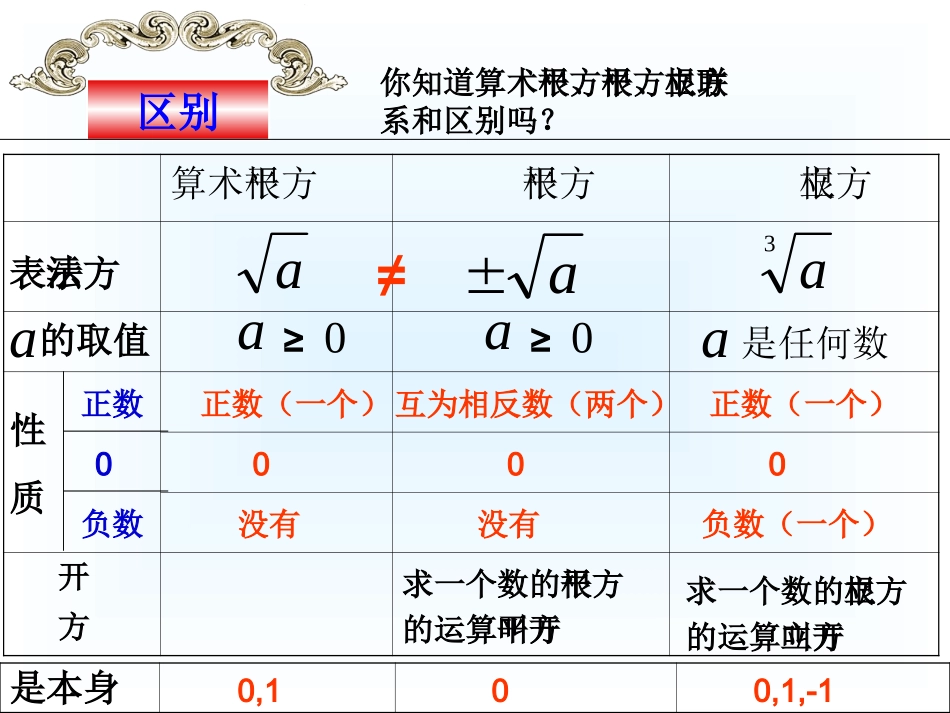
本章知识结构图乘方开方开平方开立方平方根立方根有理数无理数实数互为逆运算算术平方根负的平方根一、平方根、算术平方根和立方根的复习区别你知道算术平方根、平方根、立方根联系和区别吗？算术平方根平方根立方根表示方法a的取值性质a3aa≥0a是任何数开方a≥0a正数0负数正数（一个）0没有互为相反数（两个）0没有正数（一个）0负数（一个）求一个数的平方根的运算叫开平方求一个数的立方根的运算叫开立方≠是本身0,100,1,-1下列说法正确的是()416.的平方根是A的算术平方根的相反数表示66.B任何数都有平方根.C一定没有平方根2.aDB不要搞错了是8的平方根的平方根是64的值是64的平方根是64的立方根是6464±8884（1）0.01的平方根是（）A、0.1B、±0.1C、0.0001D、±0.0001（2）下列说法中，正确的是（）A、∵5的平方是25，∴25的平方根是5；B、∵-5的平方是25，∴25的平方根是-5；C、∵(-5)2的底数是-5，∴(-5)2没有平方根；D、∵-25是负数，∴-25没有平方根。BD3．下列说法中正确的是（）．(A)4是16的算术平方根（B）16的平方根是4(C)是6的平方根（D）-a没有平方根64．下列各式中错误的是（）．（A）（B）（C）（D）6.036.06.036.02.144.12.144.1AD两点的距离为，则，在数轴上对应的数为点，在数轴上表示的数为点BABA553（1）的倒数是；（2）－2的绝对值是；（3）若，且xy>0，x+y=。（4）332,1yx1/32－33或－354能力提高不要遗漏解下列方程：1962x2542x322）（x4)3(92y14x25x3232xx或323312yy或当方程中出现平方时，若有解，一般都有两个解体现转化的数学思想解下列方程：83x12823x12533）（y012532273）（x2x4x2y1x当方程中出现立方时，一般都有一个解体现转化的数学思想掌握规律的平方根是那么已知0017201.0,147.4201.17,311.17201.104147.0是则若已知xx,4858.0,858.46.23,536.136.2236.0的值是则已知3335250,744.35.52,738.125.538.173.计算:91692)54(36433)3(2)2(228632725.021)3(412523二、实数及分类实数的分类：有理数整数分数正整数零负整数正分数负分数无理数：无限不循环小数实数有理数集合无理数集合0.3737737773……，237722252320538940把下列各数分别填入相应的集合内：填一填_______________________________:____________________1010010001.025125089312123.1无理数有：分数有其中整数有：，，，，，，，，在____32.2随堂练习随堂练习一、判断：1.实数不是有理数就是无理数。（）2.无理数都是无限不循环小数。（）3.无理数都是无限小数。（）4.带根号的数都是无理数。（）5.无理数一定都带根号。（）6.数轴上的任何一点都可以表示实数。（）××7.平方根是本身的数是0与1.()×（1）.绝对值小于的所有整数有_______18（2）.图中阴影正方形的边长是_______（3）.在图5×5方格中，分别画出边长为的正方形.1713和2.已知正数x的平方根是m+3和2m-15,求m的值拓展提高.,10310的相反数求是整数，且，其中已知yxyxyx1.1.的值。求已知aa,033.3.的值。求已知abba,0134.4.5.5.的值。求已知abccba,02132xxxx120052005,.3对于有理数A.0B.2005C.-2005D.20051的值求已知332,aaoa的值）（）（求已知332,mnnmnm1.1.2.2.2a2a33a33a=a0a00aa)0(aaaaa0a为任何实数a为任何实数a记住公式