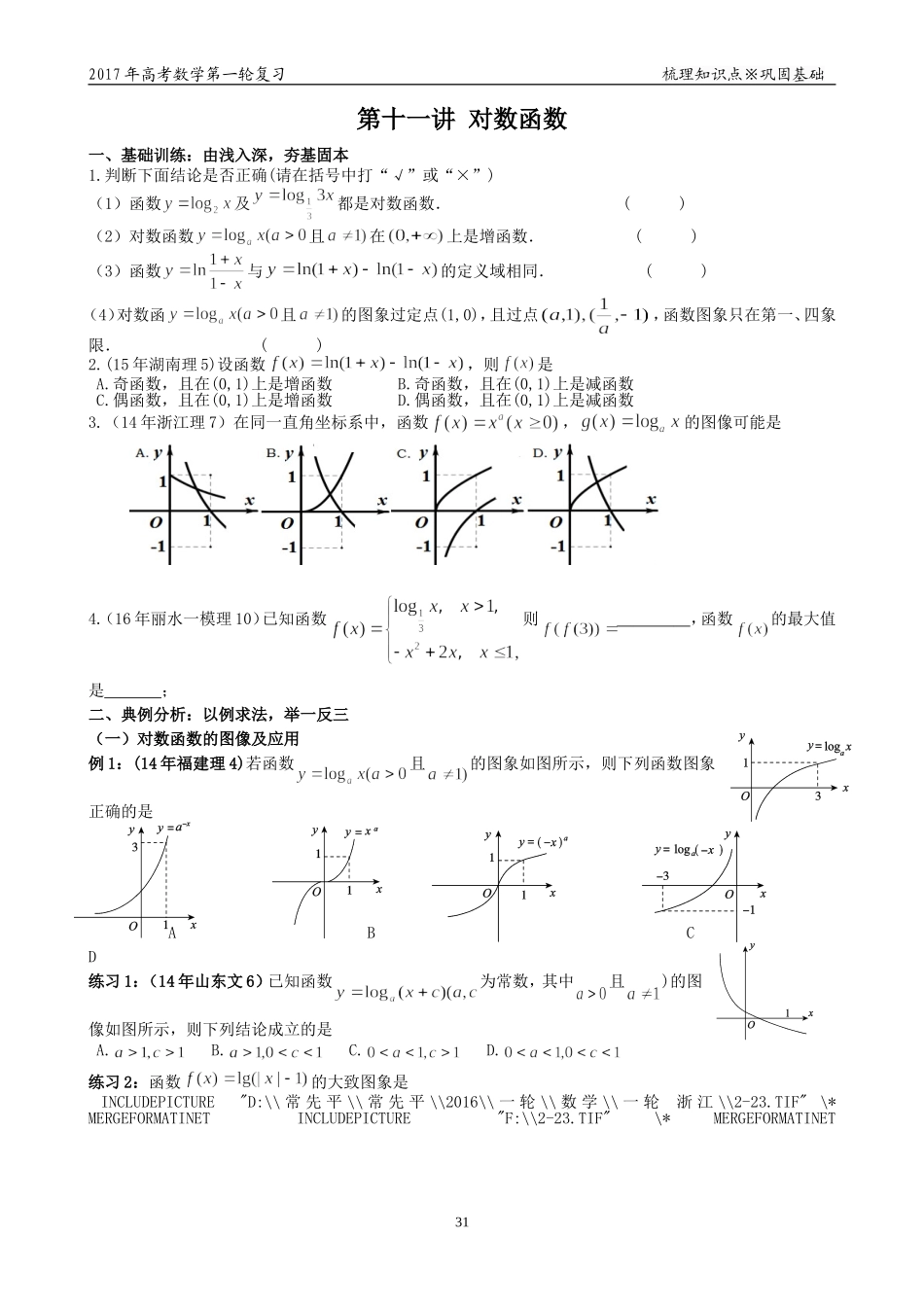
2017年高考数学第一轮复习梳理知识点※巩固基础第十一讲对数函数一、基础训练:由浅入深,夯基固本1.判断下面结论是否正确(请在括号中打“√”或“×”)(1)函数及都是对数函数.()(2)对数函数且在上是增函数.()(3)函数与的定义域相同.()(4)对数函且的图象过定点(1,0),且过点,函数图象只在第一、四象限.()2.(15年湖南理5)设函数,则是A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数3.(14年浙江理7)在同一直角坐标系中,函数,的图像可能是4.(16年丽水一模理10)已知函数则,函数的最大值是;二、典例分析:以例求法,举一反三(一)对数函数的图像及应用例1:(14年福建理4)若函数且的图象如图所示,则下列函数图象正确的是ABCD练习1:(14年山东文6)已知函数为常数,其中且)的图像如图所示,则下列结论成立的是A.B.C.D.练习2:函数的大致图象是INCLUDEPICTURE"D:\\常先平\\常先平\\2016\\一轮\\数学\\一轮浙江\\2-23.TIF"\*MERGEFORMATINETINCLUDEPICTURE"F:\\2-23.TIF"\*MERGEFORMATINET312017年高考数学第一轮复习梳理知识点※巩固基础INCLUDEPICTURE"D:\\常先平\\常先平\\2016\\一轮\\数学\\一轮浙江\\2-24.TIF"\*MERGEFORMATINETINCLUDEPICTURE"F:\\2-24.TIF"\*MERGEFORMATINET例2:已知函数,若互不相等,且,则的取值范围是A.(1,10)B.(5,6)C.(10,12)D.(20,24)练习3:(15年丽水模拟)函数在区间上的值域为,则的最小值为;练习4:(16年杭州一模理9)设函数,则___________;函数的零点是___________.方法小结:应用对数型函数的图象可求解的问题1.先求出函数的定义域,再根据函数的单调性、图像特殊点确定选项;2.对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想;3.将不等式的恒成立问题转化为函数图象的位置关系,然后画出函数的图象,根据图象求解。(二)比较对数式的大小例3:设,则的大小关系是A.B.C.D.练习5:(14年辽宁理)已知,则A.B.C.D.方法小结:比较对数值的大小的方法1.若底数为相同,则可由对数函数的单调性直接进行判断;若底数为同一字母,则需对底数进行分类讨论;2.若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较;3.若底数与真数都不同,则常借助1,0等中间量进行比较。(三)求定义域或复合函数的单调区间322017年高考数学第一轮复习梳理知识点※巩固基础例4:(14年山东理)函数的定义域为;练习6:(16年浙江调研文11)已知函数,则_______,函数的单调递减区间是_______.方法小结:1.求函数的定义域的方法:列出对应的不等式(组)求解即可.要注意对数函数的底数和真数的取值范围;2.求对数型函数的单调区间要注意底数的讨论,再利用复合函数单调性来求解。(四)解简单的对数方程或不等式例5:(16年5月湖州理10)已知函数,则;若,则实数的取值范围是;练习7:(16年嘉兴测试二理10)设函数,则=,方程的解为;方法小结:在解决与对数函数相关的比较大小或解不等式问题时,要优先考虑利用对数函数的单调性来求解.在利用单调性时,一定要明确底数的取值对函数增减性的影响,及真数必须为正的限制条件。(五)能力训练1.(16年温州一模文14)已知,若对任意的,方程均有正实数解,则实数的取值范围是;2.(16年温州一模理13)已知,若对任意的,均存在使得,则实数的取值范围是;3.(16年上海理22)已知,函数.(1)当时,解不等式;(2)若关于的方程的解集中恰好有一个元素,求的取值范围;(3)设,若对任意,函数在区间上的最大值与最小值的差不超过1,求的取值范围.332017年高考数学第一轮复习梳理知识点※巩固基础三、课后巩固:刻苦训练,练出高分1.函数的图象大致是INCLUDEPICTURE"D:\\常先平\\常先平\\2016\\一轮\\数学\\一轮浙江\\2-25.TIF"\*MERGEFORMATINETINCLUDEPICTURE"F:\\2-25.TIF"\*MERGEFORMATINETINCLUDEPICTURE"D:\\常先平\\常先平\\2016\\一轮\\数学\\一轮浙江\\2-26.TIF"\*MERGEFORMATINETINCLUDEPICTURE"F:\\2-26.TIF"\*MERGEFORMATINE...