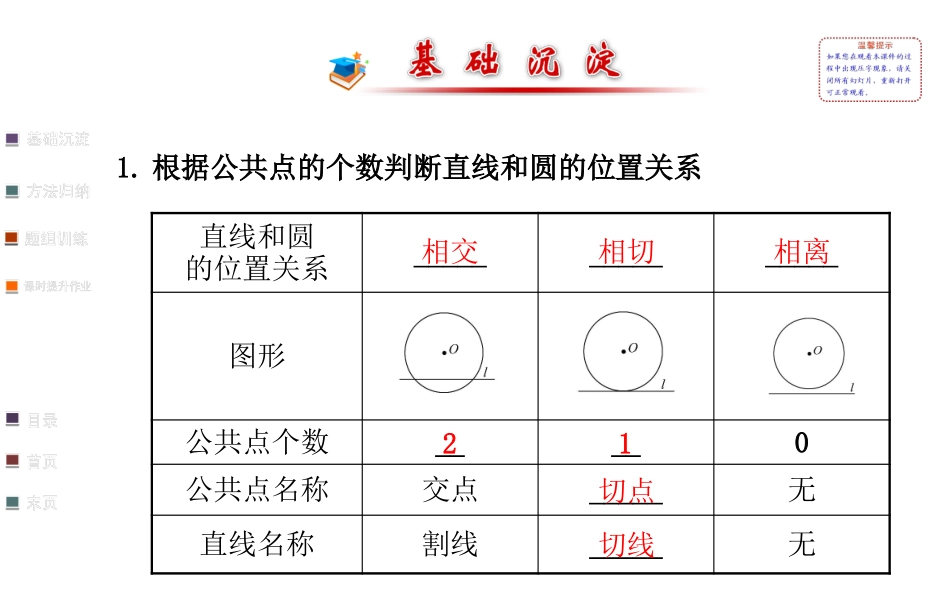
24.2.2直线和圆的位置关系第1课时播放日出视频如果把太阳看做圆,海平面看做直线,你认为圆与直线有哪些位置关系?1.根据公共点的个数判断直线和圆的位置关系直线和圆的位置关系_______________图形公共点个数____0公共点名称交点_____无直线名称割线_____无相交相切相离21切点切线2.直线和圆的位置关系与圆心到直线的距离d和半径r的关系(1)直线l和☉O相离⇔d__r.(2)直线l和☉O相切⇔d__r.(3)直线l和☉O相交⇔d__r.>=<【思维诊断】(打“√”或“×”)1.直线和圆的位置包括相交和相离.()2.直线与圆最多有两个公共点.()3.若A,B是☉O外两点,则直线AB与☉O相离.()4.圆心到直线的距离小于半径时,直线和圆相离.()5.若C为☉O内一点,则过点C的直线与☉O相交.()6.若C为☉O上的一点,则过点C的直线与☉O相切.()×√××√×知识点一直线和圆的位置关系【示范题】在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,以C为圆心,r为半径的圆与AB有何位置关系?为什么?(1)r=4cm.(2)r=4.8cm.(3)r=8cm.【思路点拨】要判定☉O与直线AB的位置关系,只需要先求出圆心C到直线AB的距离CD的长,然后再与r比较即可.【自主解答】如图,过点C作CD⊥AB于D,由勾股定理得:∵·CD·AB=·AC·BC,∴CD==4.8.(1)当r=4cm时,4<4.8,∴直线AB与⊙C相离;(2)当r=4.8cm时,4.8=4.8,∴直线AB与⊙C相切;(3)当r=8cm时,8>4.8,∴直线AB与⊙C相交.22ABACBC226810.1212ACBC68AB10【想一想】直线与圆的公共点是否能多于两个?提示:由于经过同一直线上的三点不可能作圆,因而直线与圆不可能有三个公共点,即直线与圆的公共点不可能多于两个.【微点拨】1.圆心到直线的距离是指通过圆心向直线所作的垂线段的长度.2.在没有给出圆心到直线的距离的情况下,可根据勾股定理和三角形的面积公式求出.【方法一点通】判断直线和圆的位置关系的“三个步骤”1.已知⊙O的面积为9πcm2,若点O到直线l的距离为πcm,则直线l与⊙O的位置关系是()A.相交B.相切C.相离D.无法确定2.已知圆的直径为6cm,圆心到直线l的距离为3.5cm,那么这条直线和这个圆的交点的个数是()A.0B.1C.2D.不能确定3.已知Rt△ABC的斜边AB=8cm,AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?一、必做题二、选做题三、选一道好题,明天展示