对数的运算法则VIP免费

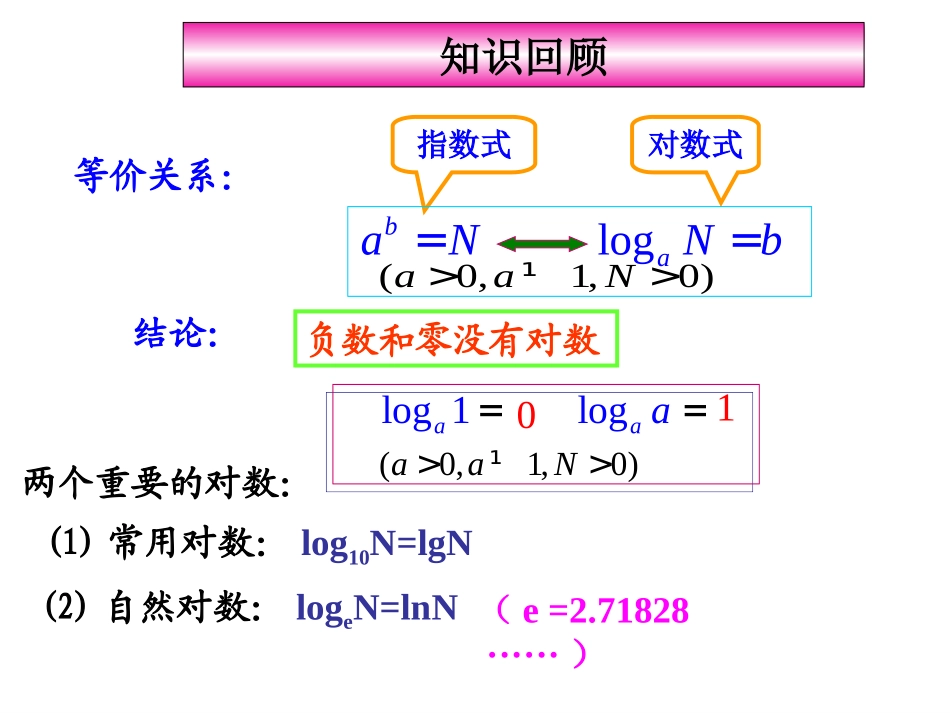
等价关系：负数和零没有对数结论：指数式对数式(1)常用对数：log10N=lgN(2)自然对数：logeN=lnN（e=2.71828······）两个重要的对数：知识回顾baN=(0,1,0)aaN>¹>logaa=log1a=01(0,1,0)aaN>¹>logaNb=(,)(,)()(,)()()mnmnmnnaamnRamnRaamnRabnR×=Î=Î=Î=Î指数运算法则知识回顾mna+mna-mnannab×问题一、研究以下两组对数求值结论求值2log4=2log8=2log(48)´=2log(48)´=3log9=3log(927)´=3log(927)´=3log27=2log82log4+3log273log9+235235探究一、两个正数的积的对数，等于同一底数的这两个数的对数的和。------（积的对数）log()loglogaaaMNMN=+（1）（积的对数等于同底对数之和）即baN=logaNb=(0,1,0)aaN>¹>log()loglogaaaMNMN=+证明：pMa=qNa=logaMp=logaNq=设，，根据对数的定义得pqpqMNaaa+==所以，log(MN)logpqaaapq+==+根据对数的定义得，log()loglogaaaMNMN=+所以，证明：log()loglogaaaMNMN=+2log(416)´=3(2)log(327)´=121(1)log(2)4´=(3)lg4lg25+=66(4)log12log3+=（积的对数）练习:例题讲解：lg5lg20+=lg(520)´=lg100=222log4log16+=24+=61422问题二、研究以下两组对数求值结论求值2log64=2log16=264log16=264log16=5log25=5log125=525log125=525log125=2log162log64-5log255log125-64223-1探究二、两个正数的商的对数，等于同一底数的被除数的对数减去除数的对数。-----（商的对数）logloglogaaaMMNN=-即（2）（商的对数等于同底对数差）baNlogaNb=(0,1,0)aaN>¹>证明：logloglogaaaMMNN=-paM=qaN=，根据对数的定义得logaMp=logaNq=设，ppqqMaaNa-==所以，loglogpqaaMapqN-==-根据对数的定义得，logloglogaaaMMNN=-所以，证明：logloglogaaaMMNN=-28(1)log4=33(2)log72log8-=（商的对数）练习：例题讲解：264(1)log4=22log64log4-=62-=433(2)log5log15-=35log15=31log3=1-12问题三、研究以下两组数据求值结论求值3log923log4=12312log9_____=´32log4=2log431log92=123log9=323log4_____=´6611探究三、一个正数的幂的对数，等于幂指数乘以这个数的对数。------（幂的对数）loglogbaaMbM=即（3）（幂的对数等于幂指数乘以此数的对数）baN=logaNb(0,1,0)aaN>¹>证明：loglogbaaMbM=paM=证明：logaMp=设，根据对数的定义得()bpbpbMaa==所以，loglogbpbaaMapb==根据对数的定义得loglogbaaMbM=所以，loglogbaaMbM=32log8=23(2)log27=5(4)lg10-=2(3)lne-=351(1)log()25=（幂的对数）练习：23log4=例题讲解：23log8=33´=932´=632log4=235log(5)-65log(5)-=56log5=-6=-513log()25=´253log5-=´523log5=-´´6=-62-5-logbaalogaba=b=对数的运算性质：log(MN)loglogaaaMN=+logloglogaaaMMNN=-loglogbaaMbM=0,10,0aaMN>¹>>且对数运算性质的综合运用：269(1)log(93)´=55(1)log20log4-=131(4)lg100log81-=23(3)log(279)´=40.8(4)lg10lnlog1e-+-=2(2)lnlogepp-+=1、例题讲解：2、练习：2699log9log3+=23+=524-=2-loga(M·N)＝logaM十logaNNMloga＝logaM－logaNlogaMn＝nlogaM积、商、幂的对数运算法则：alog(MN)loglog()logloglog()loglog()aaaaabaaMNMMNNMbM=+=-=1230,10,0aaMN>¹>>且课堂小结课堂作业：课堂作业：PP109109练习练习22、习题、习题11课后作业：本节练习册课后作业：本节练习册预习新课：§4.6对数函数预习新课：§4.6对数函数性质补充：logaNaN=logloglogcacNNa=2log3(2)2=4log5(1)4=22log3(3)2+=23(4)log9log4´=(0,1;0;0,1)aaNcc>¹>>¹练习：（证明）（证明）证明：log(0,1,0)aNaNaaN=>¹>证明：logaNax=logloglogaNaaxa=loglogaaxN=xN=logaNaN=设在等式两边取对数，即所以，即证明：logloglogcacNNa=(0,1,0,0,1)aaNcc>¹>>¹证明：，则xaN=logaNx=设loglogxccaN=c等式两边取以为底的对数loglogccxaN=即loglogccNxa=所以，logloglogcacNNa=即积、商、幂的对数运算法则：如果a>0，a1，M>0，N>0有：()()()=+=-=Îaaaaaanaalog(MN)logMlogN1MloglogMlogN2NlogMnlogM(nR)3其他重要公式:loglogmnaanNNm=logloglogcacNNa=(,(0,1)(1,),0)acNÎ+¥>loglog1abba·=,(0,1)(1,)abÎ+¥小结小结例1计算（1）)42(log752（2）27log9例题讲解例题讲解（3）237log3log7log8··例2用,logxa,logyazalog表示下列各式：32log)2(;(1)logzyxzxyaa例题讲解例题讲解（1）18lg7lg37lg214lg例3计算：解法一：18lg7lg37lg214lg18lg7lg)37lg(14lg218)37(714lg201lg)32lg(7lg37lg2)72lg(2)3lg22(lg7lg)3lg7(lg27lg2lg018lg7lg37lg214lg解法二：例题讲解例题讲解（2）例3计算：9lg243lg5lg32lg3=52=解：1133222lg27lg83lg10lg(3)lg23lg(10)(3)32lg1.2lg10+-+-=´52lg243lg3(2)lg9lg3=lg27lg83lg10(3)lg1.2+-3(lg32lg21)2lg32lg21+-=+-32=例题讲解例题讲解例4已知，求的值.a12log324log3312a例5设，已知,求的值.35abm112abm15例题讲解例题讲解.45求lg，a2lg已知b，lg3例6：例7：已知log23=a，log37=b,用a,b表示log4256解：因为log23=a，则,又∵log37=b,∴2log13a1312log7log2log37log42log56log56log33333342babab