（指数函数第一课时）VIP免费

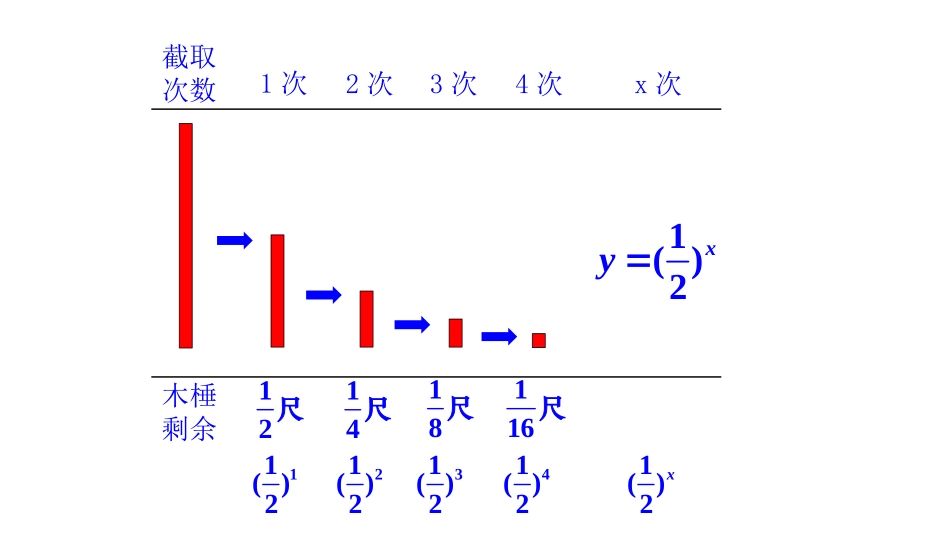
2.1.2指数函数及其性质《庄子·天下篇》中写道：“一尺之棰，日取其半，万世不竭。”请你写出截取x次后，木棰剩余量y关于x的函数关系式？情境引入截取次数木棰剩余1次2次3次4次x次12尺14尺18尺116尺1()2x1()2xy11()221()231()241()2(0,1)xyaaaxR一般地，函数叫做指数函数，其中是自变量，函数的定义域是。(1);均为幂的形式(2);底数是一个正的常数(3)x.自变量在指数位置1()2xy2xy思考：以上两个函数有什么共同特征？导入新知提示：若a=0，若a＜0，若a=1,为了避免上述各种情况，所以规定a＞0且a≠1.(0,1)xyaaaxR一般地，函数叫做指数函数，其中是自变量，函数的定义域是。函数不一定有意义。比如a=-2,y=(-2)1/2，y=(-2)1/3y=1x=1是一个常量，因此对它就没有研究的必要幂系数为1底数为正数且不为1的常数自变量仅有这一种形式注意：y=ax下列函数中是指数函数的序号是【牛刀小试】21yx（）；23xy（）；34xy（）；(4)3;xy21(5).xyx（2）用描点法作出下列两组函数的图象，然后写出其一些性质：研究函数都会研究函数图象，如何画出指数函数的图象呢？描点法是作函数图象的通用方法哦新知探究12xy2xyx-2-1.5-1-0.500.511.52y=2x0.350.711.412.83x-2-1.5-1-0.500.511.52y=2-x20.510.252442.831.4110.710.50.350.2512xy2xy011xy关于y轴对称都过定点（1,0）同坐标系中画出两函数图象，并观察图象的特点…0.0370.110.3313927…y=3-x…279310.330.110.037…y=3x…3210-1-2-3…x画出与的图象.列表：3xy1()3xy同坐标系中画出两函数图象，并观察图象的特点13xy3xy011xy关于y轴对称都过定点(1,0)与的图象.3xy1()3xy011xy12xy13xy2xy3xy011xyxy0101xyy=ax(01)（2）R上为减函数（1）过定点（0，1），即x=0时，y=1性质（0，+∞）值域R定义域图象a>100,且a≠1)的图象经过点(3,π)，求f(0)，f(1)，f(-3)的值.解析：指数函数的图象经过点(3,π)，有f(3)=π，即a3=π，解得于是13ax3fx所以101331(0)1,(1),(3)fff关键条件课堂练习【练习题1】若函数y=（a2-3a+3）ax是指数函数，则（）A．a＞1且a≠1B．a=1C．a=1或a=2D．a=2【解析】若函数y=（a2-3a+3）ax是指数函数，则a2-3a+3=1，解得a=2或a=1，又因为指数函数的底数a＞0且a≠1，故a=2.D已知指数函数f（x）的图象过点（3，8），求f（6）的值．【练习题2】【解析】设指数函数为：f（x）=ax(a>0且a≠1)，因为指数函数f（x）的图象过点（3，8），所以8=a3，所以a=2，所以f（x）=2x；所以f（6）=26=64所以f（6）的值为64．谈谈你的收获本节课学习了哪些知识？如何记忆指数函数的性质？指数函数的定义指数函数的图像及性质数形结合记住两个基本图形【思考题】【解析】指数函数的图象必过点(0,1)，即a0＝1，由此变形得a5－5＋1＝2，所以所求函数图象必过点(5,2)．(5,2)函数y＝ax－5＋1(a≠0)的图象必经过点______．2.530.10.20.33.111.7,1.7;20.8,0.8;31.7,0.9.解：(1)根据函数y=1.7x的性质，1.72.5<1.73.(2)根据函数y=0.8x的性质，0.8-0.1<0.8-0.2.(3)根据函数y=1.7x的性质，1.70.3>1.70=1，根据函数y=0.9x的性质，0.93.1<0.90=1，所以1.70.3>0.93.1根据指数函数的性质不同底的要找中间值【思考题2】比较下列各题中两个值的大小