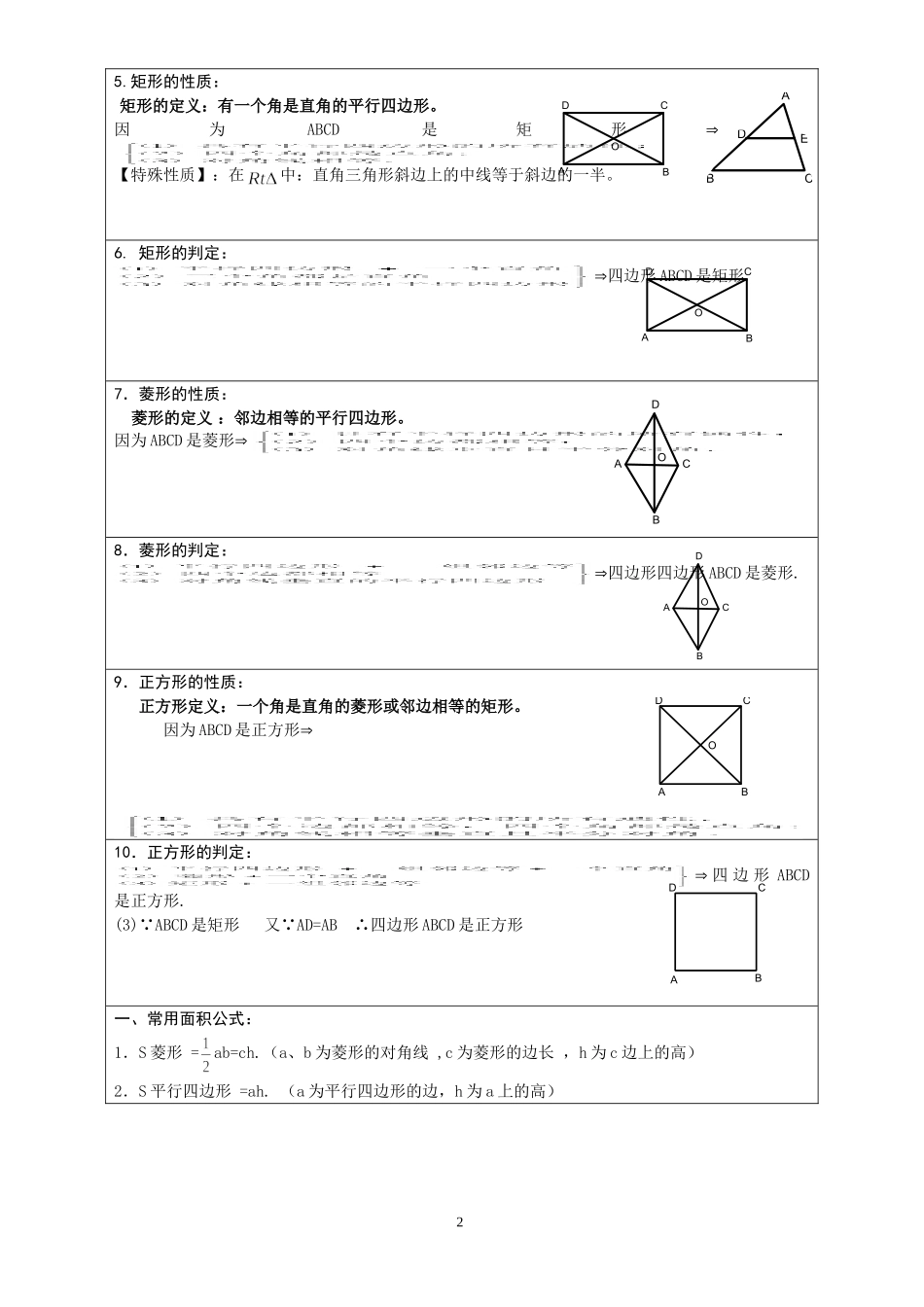
四边形知识点归纳1.多边形:在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。多边形内角和与多边形外角:内角:顶点相邻的两边所组成的角度。外角:多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。2.多边形的对角线:(1)n边形的可分为(n-2)个三角形;(2)从n边形的一个顶点可引(n-3)条对角线,共引条;(3)一个n边形截去一个角后,有(n+1)个角或n个角或(n-1)个角三种情况。2.多边形的内角和与外角和定理:(1)n边形的内角和等于(n-2)180°;正n边形的每一个内角的度数为(2)任意多边形的外角和等于360°.正n边形的每一个外角的度数为3.平行四边形的性质:平行四边形定义:有两组对边分别平行的四边形叫做平行四边形因为ABCD是平行四边形4.平行四边形的判定:.关于对称:1.平行四边形是中心对称图形,对称中心是两条对角线的交点。2.矩形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线。3.菱形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是对角线所在的直线。4.正方形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线和对角线所在的直线。11.三角形中位线定理:三角形的中位线平行第三边,并且等于它的一半。DE∥BC;DE=BC1ABCD1234ABDOCABDOCABCDOEDCBA5.矩形的性质:矩形的定义:有一个角是直角的平行四边形。因为ABCD是矩形【特殊性质】:在中:直角三角形斜边上的中线等于斜边的一半。6.矩形的判定:四边形ABCD是矩形.7.菱形的性质:菱形的定义:邻边相等的平行四边形。因为ABCD是菱形8.菱形的判定:四边形四边形ABCD是菱形.9.正方形的性质:正方形定义:一个角是直角的菱形或邻边相等的矩形。因为ABCD是正方形10.正方形的判定:四边形ABCD是正方形.(3)∵ABCD是矩形又∵AD=AB∴四边形ABCD是正方形一、常用面积公式:1.S菱形=ab=ch.(a、b为菱形的对角线,c为菱形的边长,h为c边上的高)2.S平行四边形=ah.(a为平行四边形的边,h为a上的高)2CDBAOCDBAOADBCOADBCOCDAB