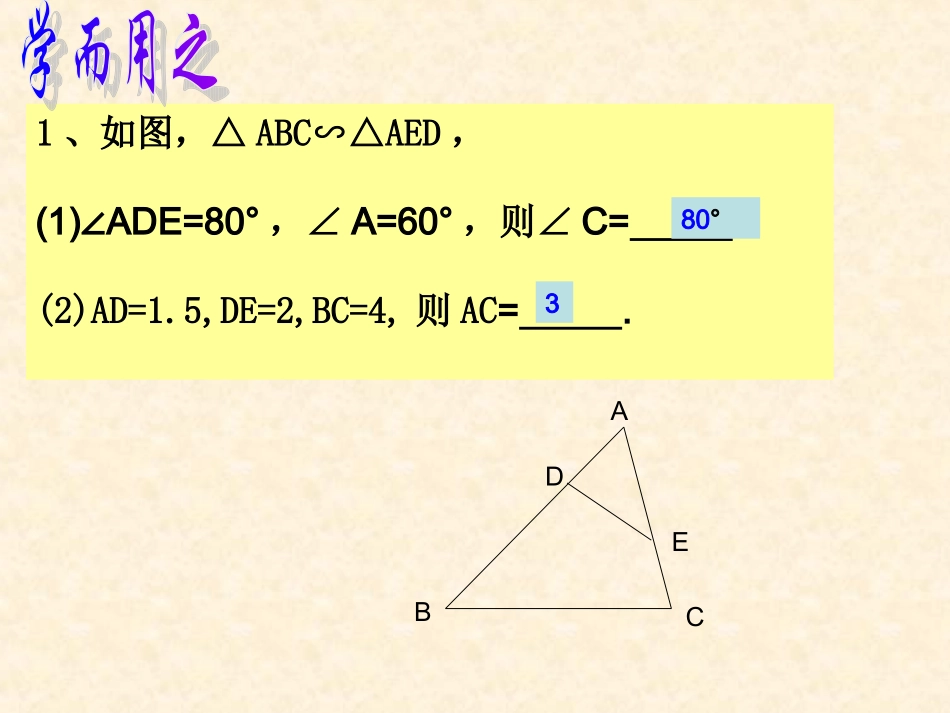
平湖市福臻中学吴燕BACB′A′C′相似三角形的对应角相等,对应边成比例.如图,∵△A′B′C′ABC∽△∴∠A′=A,B′=B,C′=C,∠∠∠∠∠ABA′B′BCB′C′ACA′C′==相似三角形的性质1、如图,△ABC∽△AED,(1)∠ADE=80°,∠A=60°,则∠C=.(2)AD=1.5,DE=2,BC=4,则AC=.EDCBA80°32、如图,在平行四边形ABCD中,AC与BD相交于点O,E为OD中点,则DF:FC等于()DA.1:4B.1:3C.2:3D.1:2EABCDOFDF:AB=?△ABEFDE∽△则AM=DN如图,△ABC≌△DEF,AM、DN分别是对应角平分线,ABCMDEFNA′B′C′D′ABCD如图,△A′B′C′∽△ABC,相似比,则对应角平分线A′D′与AD又有怎样的关系呢?kBCCB''kBCCBADDA''''A′B′C′D′ABCD如图,△A′B′C′∽△ABC,相似比,角平分线A′D′与AD,则kBCCB''kBCCBADDA''''两个相似三角形的对应角平分线之比等于相似比.高线、中线三角形的重心定义三角形三条中线的交点叫做三角形的重心。三角形的重心性质三角形的重心分每一条中线成1:2的两条线段。1、如图,在△ABC中,点E、F分别是AC、AB的中点,BE、CF相交于点G,FG=1,则CF的长为()CABCFEGA.2B.1.5C.3D.42、等腰直角三角形的腰长为,该三角形的重心到斜边的距离为.231ACBDEF3、如图,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD长为.32ABCPD3124、如图,在△ABC中,中线AD,BE相交于点F,EGBC∥,交AD于点G,求AG与GF的比.ABCDEFG三角形的重心三角形三条中线的交点叫做三角形的重心。性质:三角形的重心分每一条中线成1:2的两条线段。相似三角形的对应角相等,对应边成比例.相似三角形的性质:定义5.已知三角形ABC的边BC=8,高AD=16,矩形PQMN的四个顶点在三角形的边上,设QM为x,矩形PQMN的面积为S,求:(1)S关于的函数关系式及自变量的取值范围(2)当自变量取何值时,矩形面积最大?最大为多少?ACBDPNQM