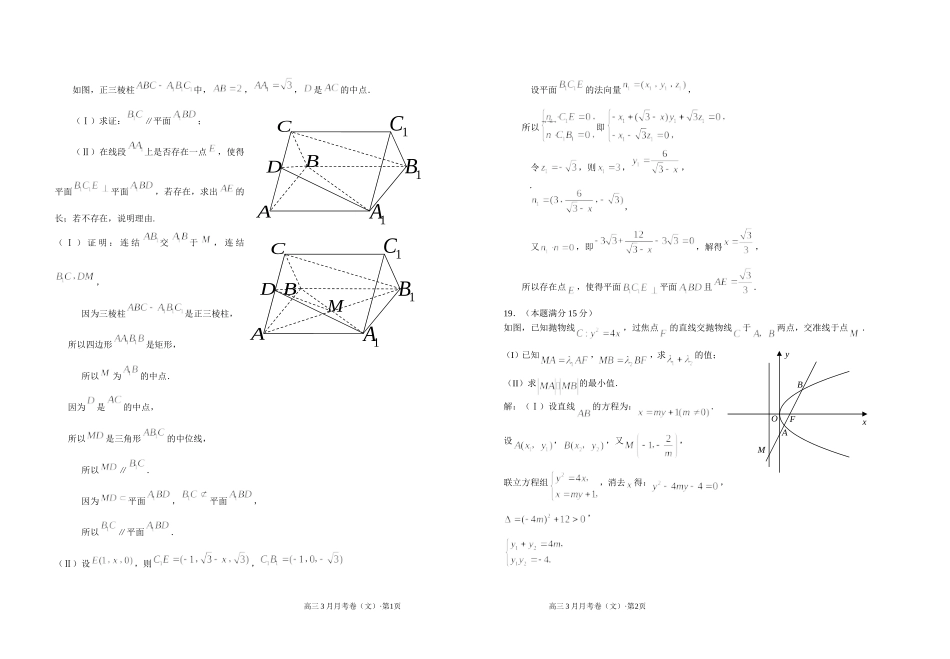
BDAECCBAD杭州第十四中学2015学年高三月考文科数学试卷答案(3月)选择题部分一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。1.(C)某几何体的三视图如图所示,则该几何体的体积为A.2B.C.4D.52.(B)已知是两个不同平面,是直线,下列命题中不正确的是A.若,,则B.若,,则C.若,,则D.若,,则3.(A)设,则“”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(A)函数2sin()1xfxx的部分图象大致为(A)(B)(C)(D)5.(A)某商店计划投入资金万元经销甲或乙两种商品.已知经销甲商品与乙商品所获得的利润分别为和(万元),且它们与投入资金(万元)的关系式,.若不管资金如何投放,经销这种商品或其中的一种商品所获得的纯利润总不小于万元,则的最小值应为A.B.C.D.6.(C)已知,若对任意,,则A.B.C.D.解:“神图”7.(D)设分别是椭圆的左、右焦点,若在直线上存在点,使线段的中垂线过点,则椭圆的离心率的取值范围是A.B.C.D.解:设,所以的中点,当,不存在,此时为中点,综上,8.(C)的边上的高线为,,(),将沿折成大小为的二面角,若,则三棱锥的侧面是A.锐角三角形B.钝角三角形C.直角三角形D.形状与a、b的值有关的三角形解法一:以△ACD为底不动,将△ABD翻折后就是二面角,由余弦定理可得又因为,所以所以△ABC为直角三角形.解法二:以△ABD为底不动,将△ACD翻折后就是二面角,因为,BD=a,CD=b,所以又因为翻折过程中保持平面平面所以平面所以所以△ABC为直角三角形.二、填空题:本大题共7小题,每小题4分,共28分.9.设全集,集合,,则集合高三3月月考卷(文)·第1页高三3月月考卷(文)·第2页正(主)视图俯视图侧(左)视图231251yxo-ππyxo-ππ-π2yxoπ2-π2yxoπ2,.解:;10.设等差数列的公差为,前n项和为.若,,则,.解:1;11.已知圆,则圆心的坐标是;若直线与圆有两个不同的交点,则的取值范围是.解:;12.函数的最小正周期为,最大值为,单调递减区间是.解:;;13.已知变量满足约束条件,则的取值范围是___________.解:14.已知正实数满足,则的最小值为.解法一:换元+不等式令,则,求的最小值所以,当且仅当时取得等号解法二:△法令所以方程有大于1的根,故解法三:转函数求值域所以15.已知正方形的边长为1,记以为起点,其余顶点为终点的向量分别为,,.若且,则的所有可能取值为.解:本题实质就是考察投影概念,所以可能取值为或三、解答题:本大题共4小题,共42分.解答应写出文字说明、证明过程或演算步骤.16.(本题满分14分)在中,角所对的边分别为,若。(Ⅰ)求的大小;(Ⅱ)设,求的值。解:(Ⅰ)由,得;(Ⅱ)由正弦定理,得:,即,解得.17.(本题满分15分)已知数列满足:,,N*).(Ⅰ)求,并求数列通项公式;(Ⅱ)记数列前2n项和为,当取最大值时,求n的值.解:(1),数列的奇数项和偶数项分别是以为公差的等差数列所以当为奇数时,当为偶数时,(II)所以当时,最大18.(本题满分15分)高三3月月考卷(文)·第1页高三3月月考卷(文)·第2页如图,正三棱柱中,,,是的中点.(Ⅰ)求证:∥平面;(Ⅱ)在线段上是否存在一点,使得平面平面,若存在,求出的长;若不存在,说明理由.(Ⅰ)证明:连结交于,连结,因为三棱柱是正三棱柱,所以四边形是矩形,所以为的中点.因为是的中点,所以是三角形的中位线,所以∥.因为平面,平面,所以∥平面.(Ⅱ)设,则,设平面的法向量,所以即令,则,,,又,即,解得,所以存在点,使得平面平面且.19.(本题满分15分)如图,已知抛物线,过焦点的直线交抛物线于两点,交准线于点.(I)已知,,求的值;(II)求的最小值.解:(Ⅰ)设直线的方程为:.设,,又,联立方程组,消去得:,,高三3月月考卷(文)·第1页高三3月月考卷(文)·第2页A1A1B1CCDBMA1A1B1CBCDBMFOAxy由,得:,,整理得:,,.解法二:由已知,,得.则:.…………①过点分别作准线的垂线,垂足分别为,,则有:.…………②由①②得:,...