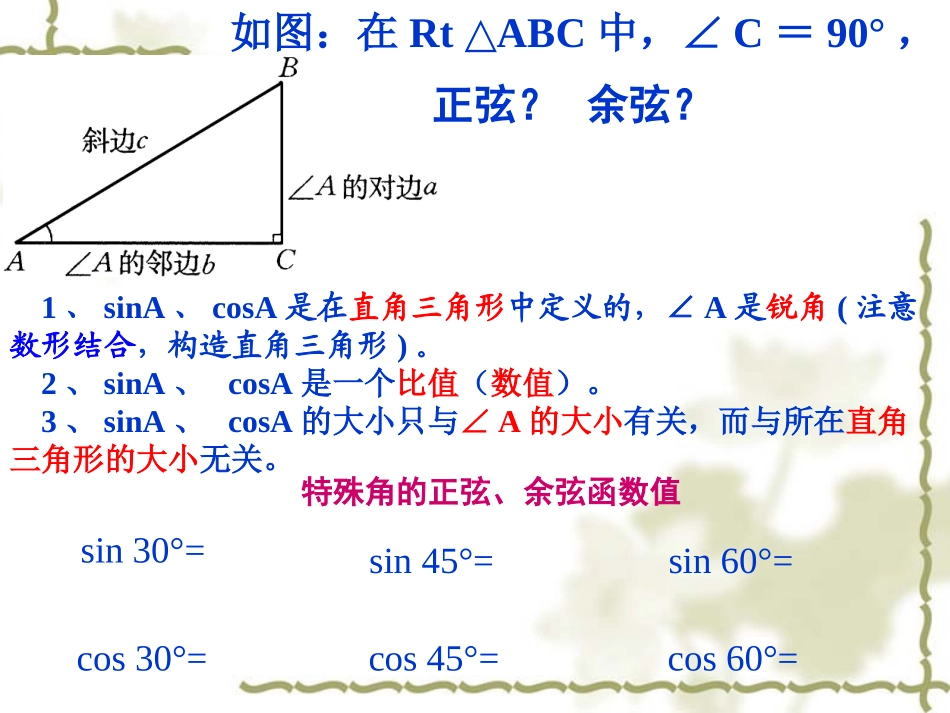
锐角三角函数——正切与余切1、sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。2、sinA、cosA是一个比值(数值)。3、sinA、cosA的大小只与∠A的大小有关,而与所在直角三角形的大小无关。如图:在RtABC△中,∠C=90°,sin30°=sin45°=sin60°=cos30°=cos45°=cos60°=特殊角的正弦、余弦函数值正弦?余弦?互为余角的正弦值与余弦值有何关系?当角度在0°~90°范围内逐渐增大时,锐角的正弦值、余弦值有何变化规律?同角的正弦值与余弦值有何关系?当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是惟一确定的吗?想一想比一比在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。B’C’BCA’C’AC=所以ACBCA’C’B’C’=即ACBCA’C’B’C’和问:有什么关系?如图:在RtABC△中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA。一个角的正切表示定值、比值、正值。我们把锐角A的邻边与对边的比叫做∠A的余切,记作cotA。abAAcotA边边的对的邻tanA×cotA=1tan30°=?33ABC┌思考:锐角A的正切值可以等于1吗?为什么?可以大于1吗?对于锐角A的每一个确定的值,sinA、cosA、tanA、cotA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切、余切叫做∠A的锐角三角函数。tan45°=tan60°=??13特殊角的三角函数值表要能记住有多好三角函数锐角α正弦sinα余弦cosα正切tanα余切cotα30045060021233332222112321333这张表还可以看出许多知识之间的内在联系?规律:①直角三角形中,锐角的大小确定后,这个角的对边与斜边的比值、邻边与斜边的比值、对边与邻边的比值随之确定。②直角三角形中,一个锐角的度数越大,它的正弦值、正切值就越大;它的余弦值、余切值就越小。1、你能得出互为余角的两个锐角A、B正切值与余切值的关系吗?2、你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?2123222123223313cotα3331结论:任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值.在在RtABC△RtABC△中中,C=90°∠,C=90°∠,,tanA=cotBtanA=cotB,,cotA=tanBcotA=tanB..cbaCBA把下列正切或余切改写成余角的余切或正切:(1)tan52°;(2)tan36°20′;(3)tan75°17′(4)cot19°;(5)cot24°48′;(6)cot15°23′.下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。试一试:试一试:ABCD(1)tanA==AC()CD()(2)tanB==BC()CD()BCADBDAC如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值()A.扩大100倍B.缩小100倍C.不变D.不能确定ABC┌C试一试:试一试:应用举例1、在RtABC△中,∠C=90°,求∠A的四个三角函数值。a=9b=122、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。3、已知∠A为锐角,sinA=,求cosA、tanA的值。1715例求下列各式的值:(1)2sin30°+3tan30°+cot45°;(2)cos45°+tan60°·cos30°.练习:求下列各式的值:(1)sin30°-3tan30°+2cos30°;(2)2cos30°+tan60°-6cot60°;(3)5cot30°-2cos60°+2sin60°;(4)cos245°+sin245°;2填空:=则锐角若=则锐角若,1cot47tan)3(,1tan35tan)2(55tan45tan35tan)1(定义中应该注意的几个问题:回味无穷1、sinA、cosA、tanA、cotA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。2、sinA、cosA、tanA,cotA是一个比值(数值)。3、sinA、cosA、tanA,cotA的大小只与∠A的大小有关,而与直角三角形的大小无关。同角三角函数关系式互为余角的三角函数之间的关系AAAcossintan1cossin22AAAAtan1cottanA.Acot(90cotBcotA,Atan(90tanBsinA,Acos(90cosBcosA,A)=-)=-)=-)=-90sin(sinB回顾:sinA+cosA>10<sinA<1,0<cosA<1,