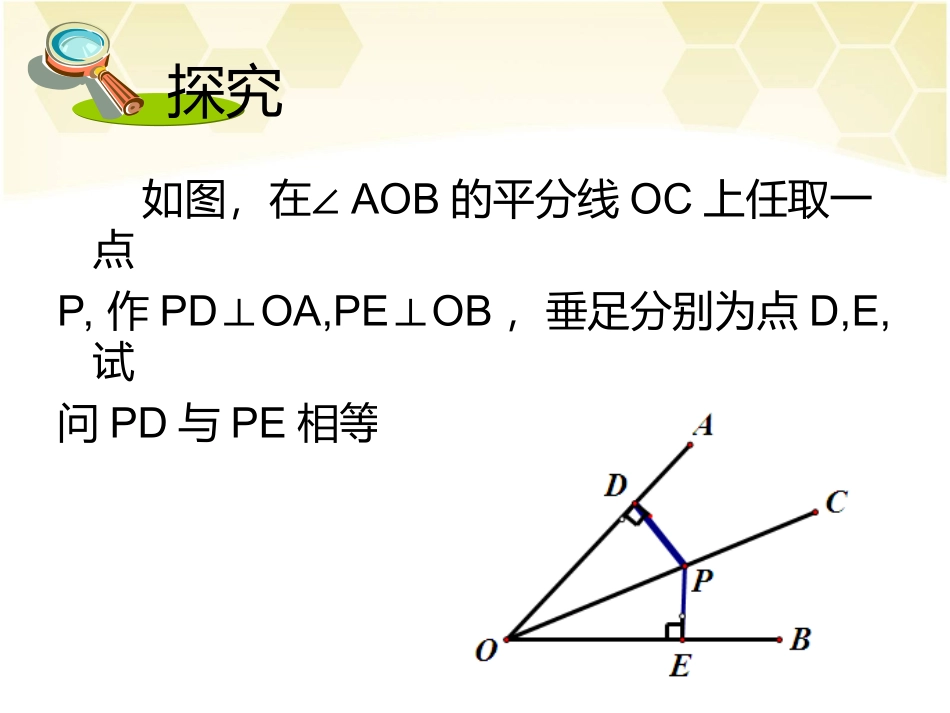
1.4角平分线的性质第1课时角平分线的性质角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.探究如图,在∠AOB的平分线OC上任取一点P,作PDOA,PEOB⊥⊥,垂足分别为点D,E,试问PD与PE相等吗?你能证明吗?你能证明吗?将∠AOB沿OC对折,我发现PD与重合,即PD与PE相等将∠AOB沿OC对折,我发现PD与重合,即PD与PE相等我们来证明这个结论:∵PDOA,PEOB,⊥⊥∴∠PDO=PEO=90°.∠在△PDO和△PEO中,∵∠PDO=PEO∠,∠DOP=EOP∠,OP=OP,∴△PDOPEO.≌△∴PD=PE.由此得到角平分线的性质定理:角的平分线上的点到角的两边的距离相等.角的内部到角的两边距离相等的点在这个角的平分线上吗?如图,点P在∠AOB的内部,作PDOA⊥,PEOB,⊥垂足分别为点D,E.若PD=PE,那么点P在∠AOB的平分线上吗?动脑筋如图,过点O,P作射线OC.∵PDOA⊥,PEOB,⊥∴∠PDO=PEO=90°.∠在RtPDO△和RtPEO△中,∵OP=OP,PD=PE,∴RtPDORtPEO.△≌△∴∠AOC=BOC.∠∴OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.由此得到角平分线的性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.例1如图,∠BAD=BCD=90°∠,∠1=2.∠(1)求证:点B在∠ADC的平分线上;(2)求证:BD是∠ABC的平分线上.证明(1)在△ABC中,∵∠1=2∠,∴BA=BC.又BAAD,BCCD,⊥⊥∴点B在∠ADC的平分线上.例题例题(2)在RtBAD△和RtBCD△中,∵BA=BC,BD=BD,∴RtBAD△和RtBCD.△∴∠ABD=CBD.∠∴BD是∠ABC的平分线.1.如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等.练习解:作∠AOB的平分线,∠AOB的平分线与MN交于一点,如图1所示:点P即为所求.图12.如图,在△ABC中,AD平分∠ABC,DE⊥AB于点E,DF⊥AC于点F,BD=CD.求证:AB=AC.证明:∵AD平分∠ABC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF.∵BD=CD,∴Rt△DBE≌Rt△DCF.∴∠B=∠C.∴AB=AC.•今天这堂课学了什么内容?反思小结1.角平分线上的点到角的两边的距离相等.2.角的内部到角的两边距离相等的点在角的平分线上.