北师大版八年级数学(上)第三章证明(三)平行四边形(三)VIP免费

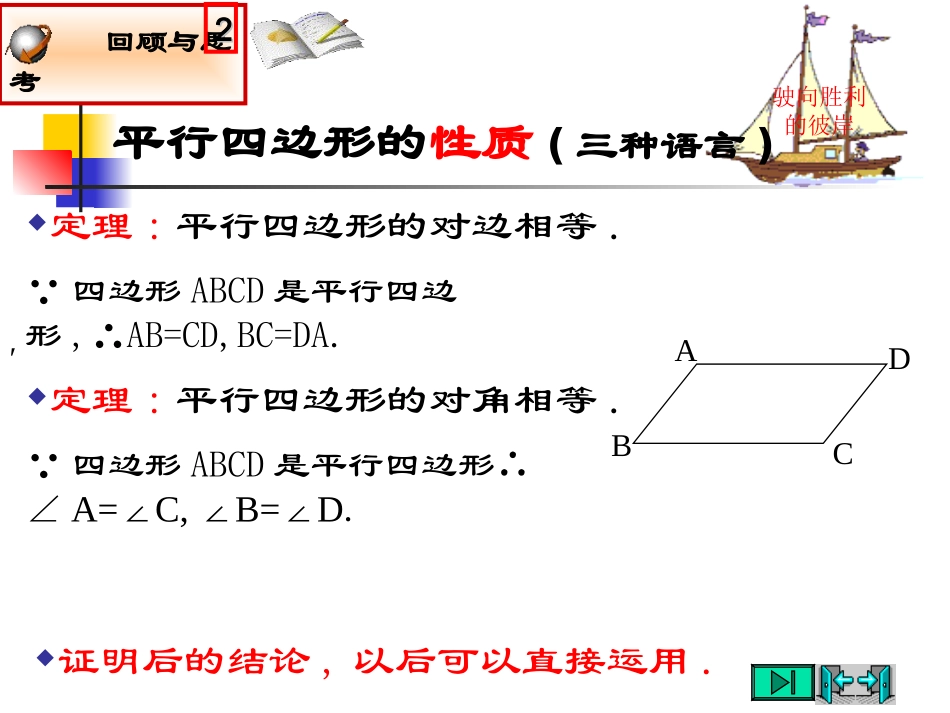
九年级数学(上)第三章证明(三)1.平行四边形(3)平行四边形的判定渭南经开区龙背初中严静学好几何标志是会“证明”证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.回顾与思考11驶向胜利的彼岸定理:平行四边形的对边相等.′驶向胜利的彼岸证明后的结论,以后可以直接运用.BDCA 四边形ABCD是平行四边形,∴AB=CD,BC=DA.定理:平行四边形的对角相等. 四边形ABCD是平行四边形∴∠A=C,B=D∠∠∠.平行四边形的性质(三种语言)回顾与思考22平行四边形的性质(三种语言)′驶向胜利的彼岸证明后的结论,以后可以直接运用.定理:平行四边形的对角线互相平分. 四边形ABCD是平行四边形∴CO=AO,BO=DO.BDCAO定理:夹在两条平行线间的平行线段相等. MN∥PQ,AB∥CD,∴AB=CD.BDCAMNPQ回顾与思考33驶向胜利的彼岸等腰梯形的性质(三种语言)定理:等腰梯形同一底上的两个角相等.定理:等腰梯形的两条对角线相等.在梯形ABCD中,AD∥BC, AB=DC,∴AC=DB..在梯形ABCD中,AD∥BC, AB=DC,∴∠A=D,B=C∠∠∠.BDCABDCA证明后的结论,以后可以直接运用.回顾与思考44驶向胜利的彼岸等腰梯形的判定(三种语言)定理:同一底上的两个角相等的梯形是等腰梯形.在梯形ABCD中,AD∥BC, ∠A=D∠或∠B=C∠,∴AB=DC.定理:两条对角线相等的梯形是等腰梯形.在梯形ABCD中,AD∥BC, AC=DB.∴AB=DC.BDCABDCA证明后的结论,以后可以直接运用.回顾与思考55驶向胜利的彼岸平行四边形的判定P77行家看门道11定理:两组对边分别相等的四边形是平行四边形.BDCA已知:如图,在四边形ABCD中,AB=CD,BC=DA..求证:四边形ABCD是平行四边形.分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而作辅助线,用全等三角形来证明相应的角相等.证明:连接AC. AB=CD,BC=DA,AC=CA,∴△ABC≌△CDA(SSS).∴∠1=∠2,∠3=∠4.∴AB∥CD,CB∥AD.∴四边形ABCD是平行四边形.1234平行四边形的判定P78定理:一组对边平行且相等的四边形是平行四边形.′驶向胜利的彼岸议一议22已知:如图,在四边形ABCD中,AB∥CD,AB=CD.求证:四边形ABCD是平行四边形.分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别相等,从而作辅助线,用全等三角形来证明相应的边相等.证明:连接AC. AB∥CD,∴∠1=∠2. AB=CD,AC=CA,∴△ABC≌△CDA(SAS)..∴四边形ABCD是平行四边形.∴BC=DA.BDCA12你还有不同的证法吗?平行四边形的判定P78驶向胜利的彼岸随堂练习33定理:对角线互相平分的四边形是平行四边形.已知:如图,在四边形ABCD中,对角线AC,BD相交于点O,CO=AO,BO=DO.求证:四边形ABCD是平行四边形.证明: CO=AO,BO=DO,∠1=∠2,∴△AOD≌△COB(SAS).∴∠3=∠4.∴AD∥CB.同理,AB∥CD.∴四边形ABCD是平行四边形.BDCAO分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而用全等三角形来证明相应的角相等.你还有几种不同的证法?4321平行四边形的判定P79′驶向胜利的彼岸我思,我进步44定理:两组对角分别相等的四边形是平行四边形的.已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行.从而转化为相关的角关系来证明.证明: ∠A=∠C,∠B=∠D,∠A+∠C+∠B+∠D=3600.∴∠A+∠B=1800.∴AD∥BC.BDCA∴2∠A+2∠B=3600.同理,AB∥CD.∴四边形ABCD是平行四边形.谁是“联想总裁”?做一做55′驶向胜利的彼岸已知:如图.求证:四边形MNOP是平行四边形.分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.证明:OMNP45x-311-xx-5.453222xx.8x.5POMN.3ONPM∴四边形MNPO是平行四边形.是金子,总会发光随堂练习66′驶向胜利的彼岸已知:如图,在□ABCD中,BF=DE.求证:四边形AFCE是平行四边形.分析:由已知的平行四边形和BF=DE可知,CE=AF,...