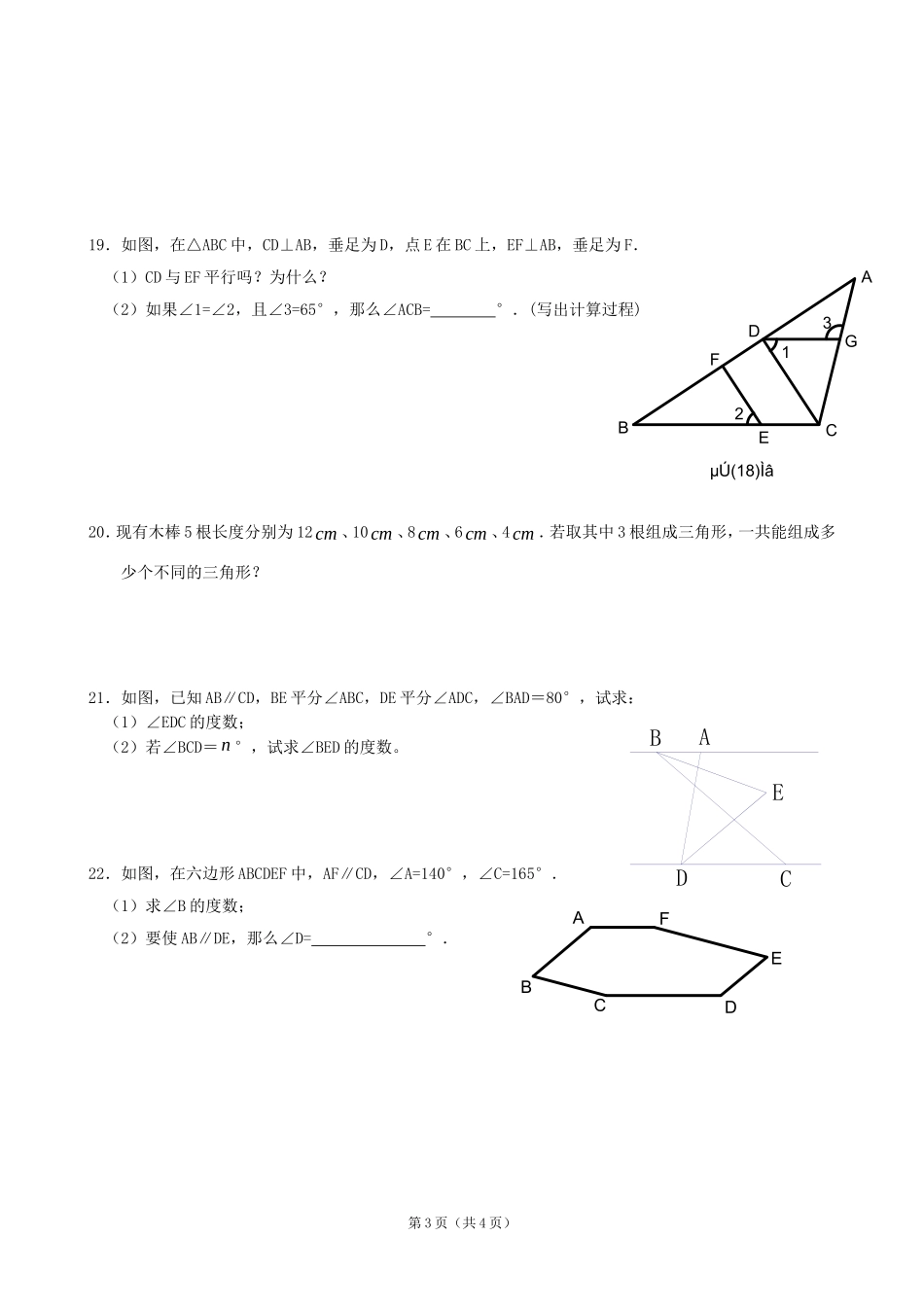
第(1)题DCBA(A)(C)(D)(B)(A)DCBA(B)DCBA(C)DCBA(D)DCBA21第(8)题21GFEDCBA第(9)题cba21DCBA第七章平面图形的认识(二)测试题班级姓名一、选择题:(每小题5分,共35分)1.如图,下列说理中,正确的是()(A)因为∠A+∠D=180°,所以AD∥BC(B)因为∠C+∠D=180°,所以AB∥CD(C)因为∠A+∠D=180°,所以AB∥CD(D)因为∠A+∠C=180°,所以AB∥CD2.一个多边形的每个内角都等于108°,则此多边形是()(A)五边形(B)六边形(C)七边形(D)八边形3.下列图形中,不能通过其中一个四边形平移得到的是()4.已知三角形的两边分别为4和9,则此三角形的第三边可能是()(A)4(B)5(C)9(D)135.在下列各图的△ABC中,正确画出AC边上的高的图形是()6.将一张长方形纸片如图所示折叠后,再展开.如果∠1=56°,那么∠2等于()(A)56°(B)68°(C)62°(D)66°7.如图,AB∥CD,且∠ACB=90°,则与∠CAB互余的角有()个(A)1个(B)2个(C)3个(D)4二、填空题(每空2分,共26分)8.如图,∠1、∠2是两条直线和被第三条直线所截的角.9.如图,两条平行线a、b被直线c所截.若∠1=118°,则∠2=°.第1页(共4页)第(10)题EDCBA第(12)题DCBA432110.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠BAD=°,∠EAD=°.11.将△ABC向左平移10cm得到△DEF,若∠ABC=52°,则∠DEF=°,CF=cm.12.如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是.(填一个你认为正确的条件即可)13.直角三角形中两个锐角的差为20°,则两个锐角的度数分别为°,°.14.在△ABC中,如果∠B=45°,∠C=72°,那么与∠A相邻的一个外角等于°.三、解答题(第15~18题各8分,第19、20题各9分,第21—23题各10分,共88分)15.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.16.如图,在△ABC中,∠BAC是钝角.(1)画出边BC上的中线AD;(2)画出边BC上的高AH;(3)在所画图形中,共有个三角形,其中面积一定相等的三角形是.17.如图,AB∥CD,∠B=61°,∠D=35°.求∠1和∠A的度数.18.如图,AB∥DE,∠A=∠D.AC与DF平行吗?请说明理由.第2页(共4页)µÚ(15)ÌâCBAµÚ(16)ÌâEDCBA1µÚ(17)ÌâGFEDCBAECDBA19.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.(1)CD与EF平行吗?为什么?(2)如果∠1=∠2,且∠3=65°,那么∠ACB=°.(写出计算过程)20.现有木棒5根长度分别为12cm、10cm、8cm、6cm、4cm.若取其中3根组成三角形,一共能组成多少个不同的三角形?21.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:(1)∠EDC的度数;(2)若∠BCD=n°,试求∠BED的度数。22.如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°.(1)求∠B的度数;(2)要使AB∥DE,那么∠D=°.第3页(共4页)µÚ(18)Ìâ321GFEDCBAFEDCBA23.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=°,∠3=°.(2)在(1)中,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°.(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?第4页(共4页)321nmba