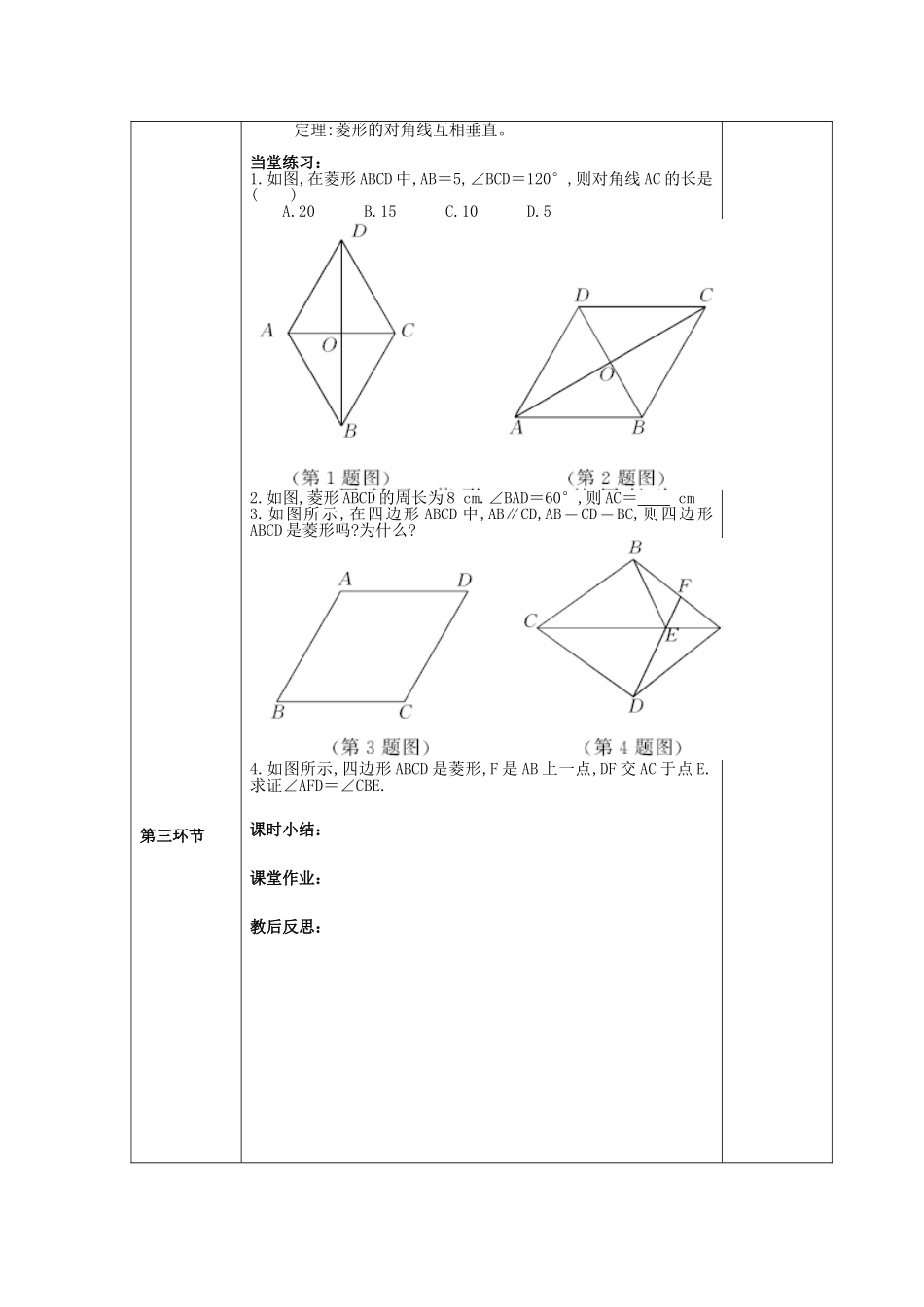
教学目标教学重点教学难点教学过程第一环节第二环节1.1菱形的性质与判定(第1课时)主备人:孙志昂1.探索并掌握菱形的概念和菱形所具有的特殊性质,会进行简单的推理和运算.1.菱形的概念和性质.1.菱形性质的灵活应用.导入新课:请同学们观察图片中的四边形并回答下列问题:(1)图片中有平行四边形吗?(2)这些平行四边形具有哪些特征?其中哪个特征不是平行四边形的性质?探究新知:1.今天我们来学习一种特殊的平行四边形,让我们一起观察、猜想、探究、归纳、论证吧!结合上面的观察,你能举出和上述图形具有相同特征的实物图形吗?具有这一特征的平行四边形是什么四边形?结论:有一组邻边相等的平行四边形叫做菱形。1.菱形是特殊的平行四边形,它具有一般平行四边形的所有性质.你能列举一些这样的性质吗?结论:菱形的对边平行且相等,对角相等,对角线互相平分。2.菱形还具有什么性质那?请同学们用菱形纸片折一折,回答下列问题:(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?(2)菱形中有哪些相等的线段?结论:(1)菱形是轴对称图形,有两条对称轴,且是菱形的两条对角线所在的直线,两条对称轴互相垂直。(2)菱形的四条边相等。3.证明菱形性质如图所示,在菱形ABCD中,已知AB=AD,对角线AC与BD相交于点O.求证:(1)AB=BC=CD=AD;(2)AC⊥BD.5.定理:菱形的四条边相等。二次备课第三环节定理:菱形的对角线互相垂直。当堂练习:1.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是()A.20B.15C.10D.52.如图,菱形ABCD的周长为8cm.∠BAD=60°,则AC=cm3.如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,则四边形ABCD是菱形吗?为什么?4.如图所示,四边形ABCD是菱形,F是AB上一点,DF交AC于点E.求证∠AFD=∠CBE.课时小结:课堂作业:教后反思:第四环节第五环节第六环节