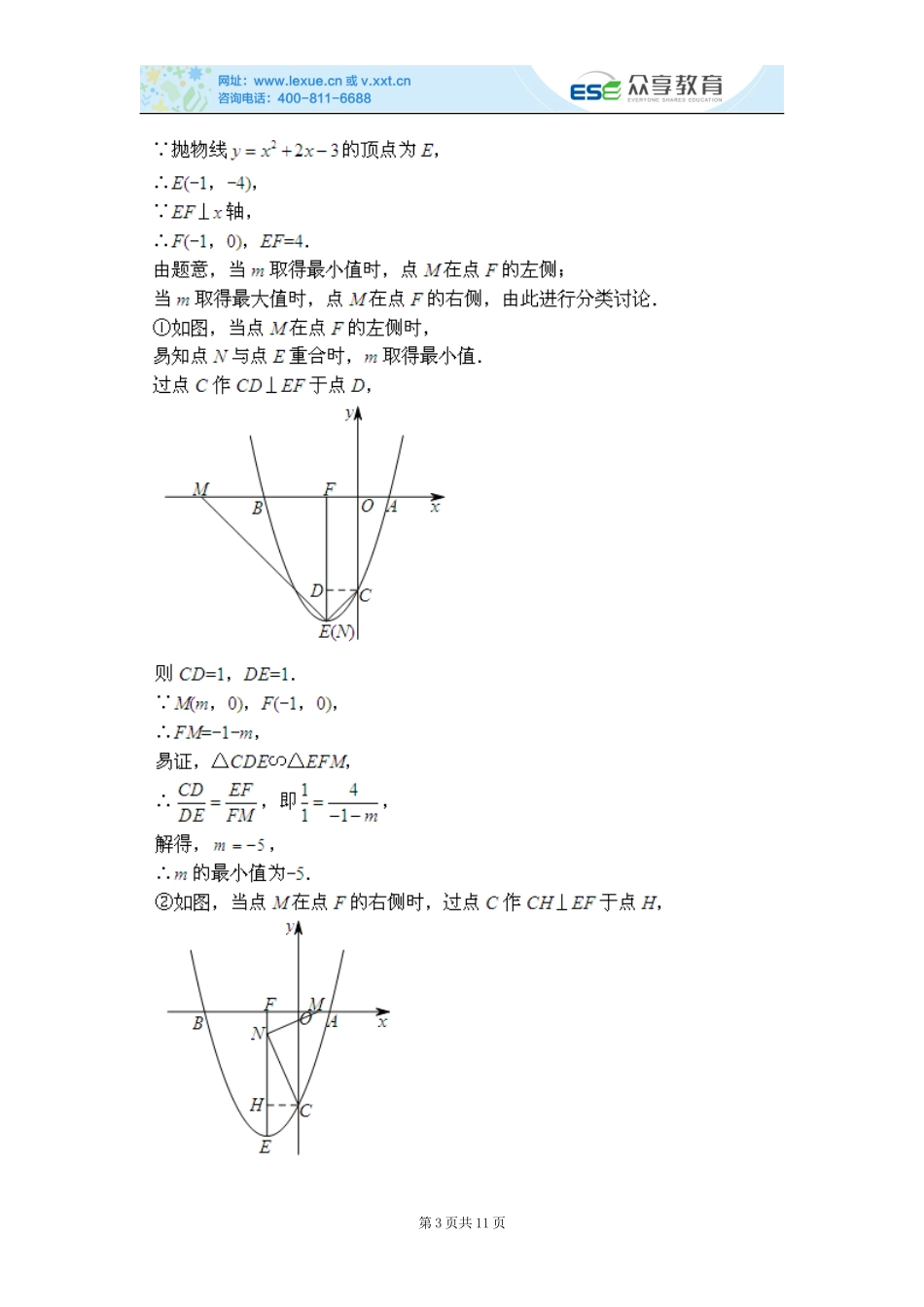
学生做题前请先回答以下问题问题1:常用函数处理手段(设计方案时常使用的手段)有哪些?问题2:见到直角我们都有哪些思考角度?问题3:怎么根据题目特征选取适当的直角思考角度?举例说明.问题4:正方形的存在性通常转化成什么问题来处理?问题5:(两定一动)等腰直角三角形存在性问题的处理思路是什么?直角的思考角度一、单选题(共5道,每道15分)1.如图,抛物线经过A,B,C三点,已知A(1,0),C(0,-3).(1)抛物线的解析式为()A.B.C.D.答案:C解题思路:试题难度:三颗星知识点:二次函数的表达式第1页共11页2.(上接第1题)(2)已知抛物线的顶点为E,EFx⊥轴于点F,M(m,0)是x轴上一点,N是线段EF上一点.若∠MNC=90°,则m的取值范围是()A.B.C.D.答案:B解题思路:第2页共11页第3页共11页试题难度:三颗星知识点:斜直角的处理思路(斜转直)3.如图1,以一块等腰直角三角板的两条直角边为坐标轴建立平面直角坐标系,已知OA=OB=3,过点A,B的抛物线的对称轴为直线x=1,抛物线与x轴的另一交点为D.(1)抛物线的解析式为()A.B.C.D.答案:D解题思路:第4页共11页试题难度:三颗星知识点:二次函数的表达式4.(上接第3题)(2)如图2,将三角板的直角顶点C在x轴上滑动,一直角边所在直线过点B,另一直角边所在直线与抛物线的交点为E,若点E的横坐标为4,则点C的坐标为()A.B.C.D.答案:C解题思路:第5页共11页第6页共11页试题难度:三颗星知识点:三等角模型5.(上接第3,4题)(3)如图3,若P为抛物线对称轴上一点,N为坐标平面内一点,且在x轴上方的抛物线上存在点M,使得以A,P,M,N为顶点的四边形是正方形,则点M的坐标为()第7页共11页A.B.C.D.答案:D解题思路:第8页共11页第9页共11页第10页共11页试题难度:三颗星知识点:正方形的存在性第11页共11页