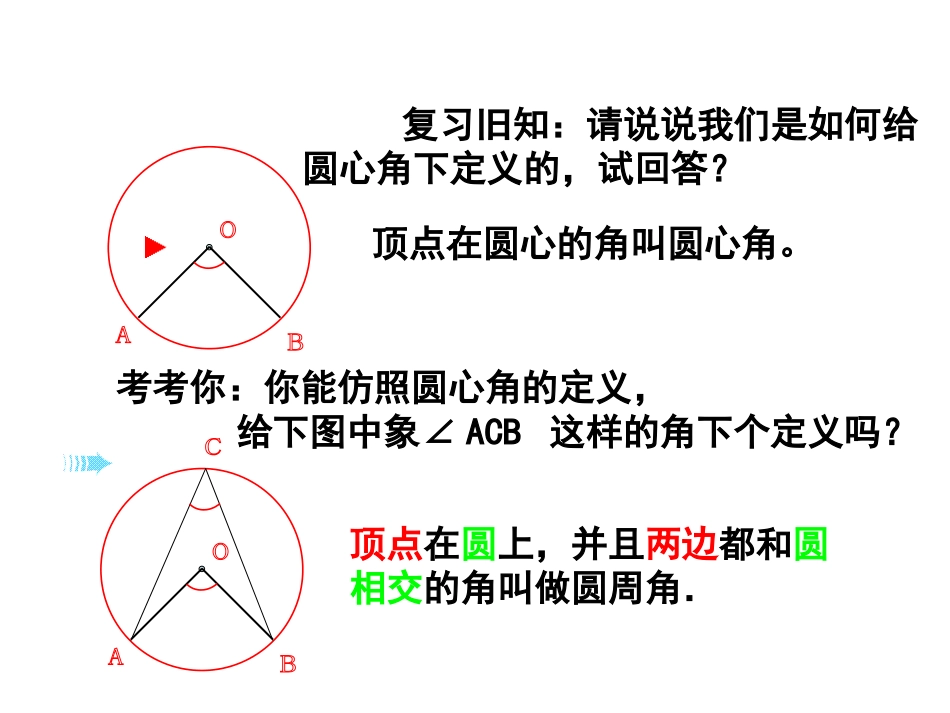
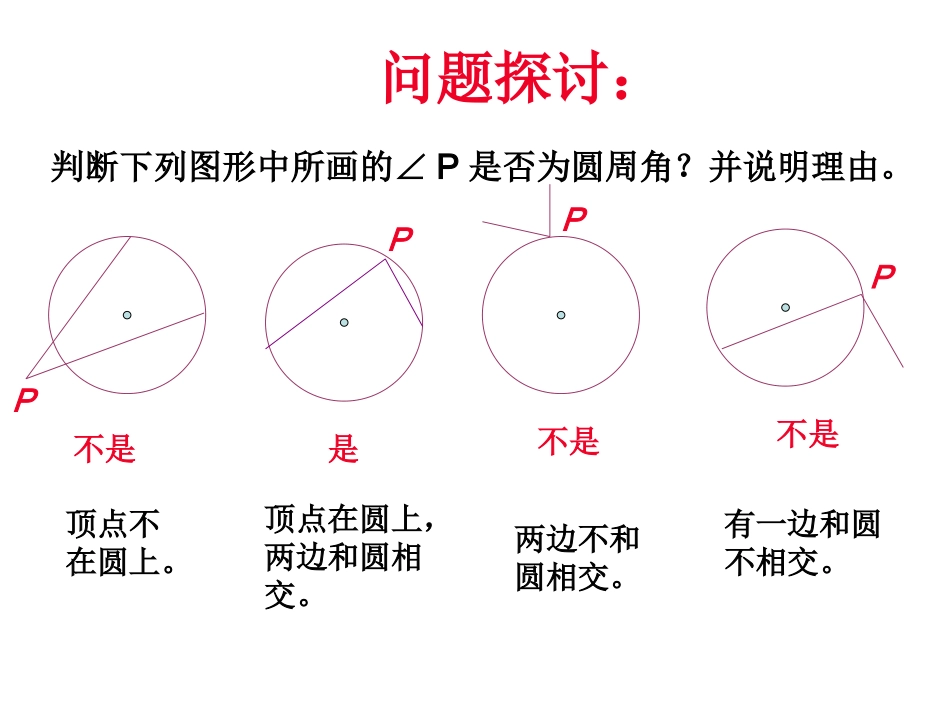
24.1.4圆周角复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角。考考你:你能仿照圆心角的定义,给下图中象∠ACB这样的角下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角.问题探讨:判断下列图形中所画的∠P是否为圆周角?并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上,两边和圆相交。两边不和圆相交。有一边和圆不相交。•当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?.BACDE生活实践E●OBDCA你能发现什么规律?AC所对的圆周角∠AECABC∠∠ADC的大小有什么关系?⌒画一个圆,再任意画一个圆周角,看一下圆心在什么位置?圆心在一边上圆心在角内圆心在角外观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?结论:圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。结论:圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,等于这条弧度数的一半,这条弧所对的圆心角的一半在同圆或等圆中,若圆周角相等,那么所对弧相等。巩固练习:如图,点A,B,C,D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678问题1:如图,AB是⊙O的直径,请问:∠C1、∠C2、∠C3的度数是。ABOC1C2C3推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。问题2:若∠C1、∠C2、∠C3是直角,那么∠AOB是。90°180°探究与思考:第二课时应用•回顾:圆周角定理及推论?·ABC1OC2C3归纳:定理在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.定理半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.在同圆或等圆中,相等的圆周角所对的弧相等推论练一练1、如图,在⊙O中,∠ABC=50°,则∠AOC等于()A、50°;B、80°;C、90°;D、100°ACBOD2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于()A、30°;B、60°;C、90°;D、45°CABPB练一练3、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是。CABO解:连接OA、OB∵∠C=30°,∴∠AOB=60°又∵OA=OB,∴△AOB是等边三角形∴OA=OB=AB=2,即半径为2。2ABCOABCOABCOABCODABCOD4、下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。例如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.86102222ACABBC又在Rt△ABD中,AD2+BD2=AB2,221052(cm)22ADBDAB解:∵AB是直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD..ACDBCD例题OABCD•弦AB把圆周分成1:2的两部分,已知半径为1,求弦长ABABO定义:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做多边形的外接圆。ACBO·图1ABCD探讨:1、(1)如图1,在⊙O上任取三点A、B、C,连结AB、BC、CA,则△ABC叫做⊙O的______三角形,⊙O叫做△ABC的________圆。ACBO·图1(2)图1中的∠A、∠B、∠C都是⊙O的______角,若∠A=42°,则=°,=°。276内接外接圆周842、如图,点A、B、C、D在⊙O上,若优弧ABC为2600,则∠D=__若弧AC为100º则∠B=__,∠B+D=__,A+C=___∠∠∠∠DCE和∠A有什么关系?ABCDBCDAE圆的内接四边形的对角互补,并且任何一个外角等于它的内对角课堂练习•1.如图,OA、OB、OC都是⊙O的半径,∠AOB=2BOC∠,∠ACB与∠BAC的大小有什么关系?为什么?OABC课堂练习•2.如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD和∠BAD的大小。OBDCA当堂检测2.如图,圆心角∠AOB=100°,则∠ACB=___。OABCBAO.70°x1.求圆中角X的度数AO.X120°AO.X120°CCDB1、x=35°x=120°2、∠ACB=130°3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.·ABCO求证:△ABC为直角三角形.证明:CO=AB,12以AB为直径作⊙O,∵AO=BO,∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.12已知:△ABC中,CO为AB边上的中线,12且CO=AB∴△ABC为直角三角形.思考题