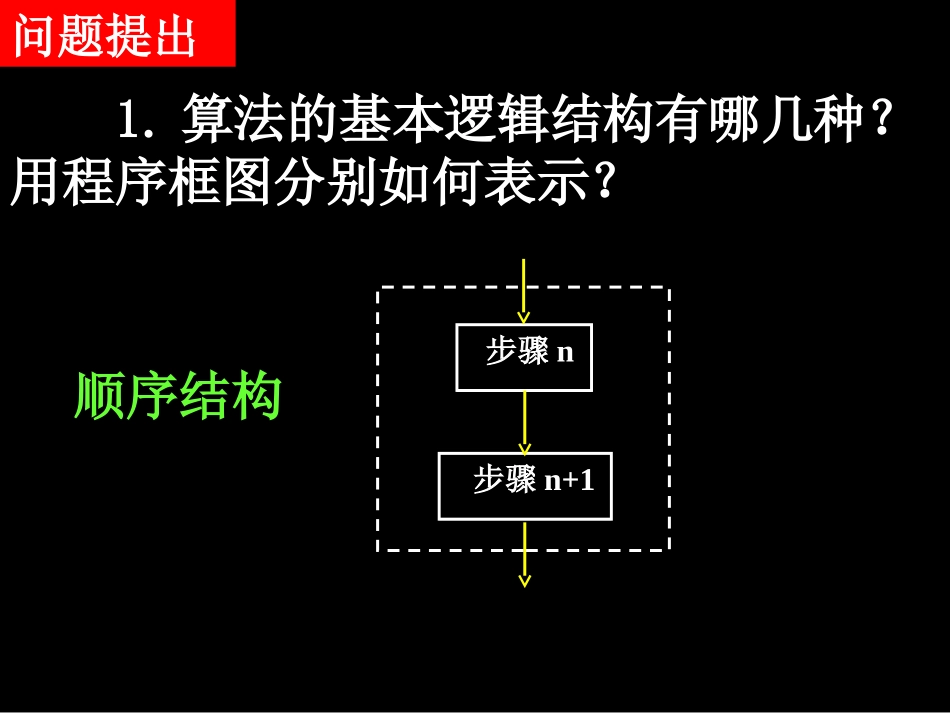
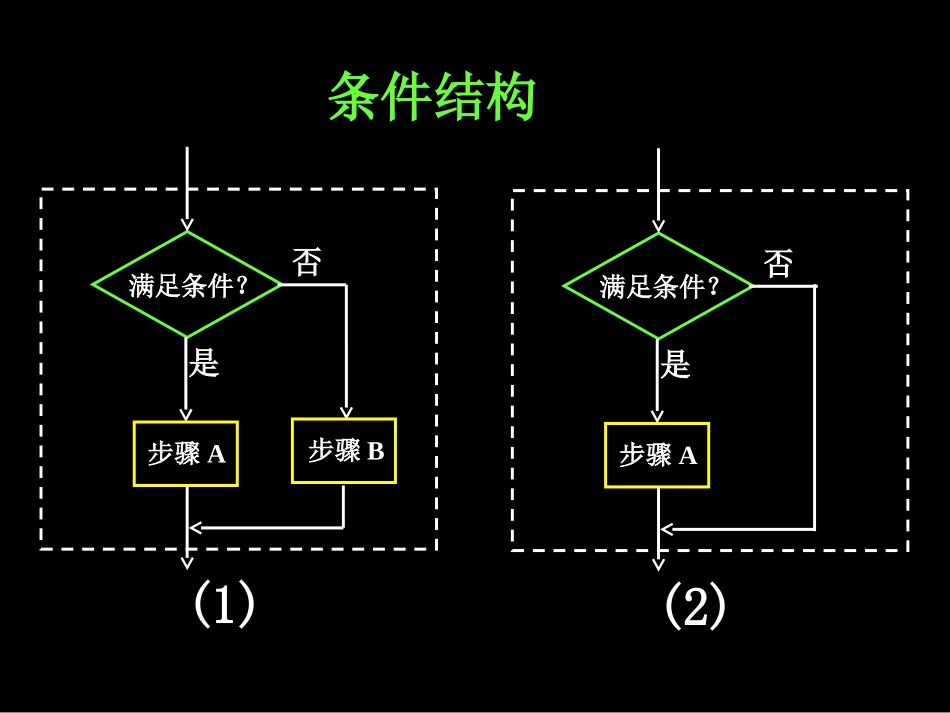
1.1.2程序框图与算法的基本逻辑结构习题课问题提出1.算法的基本逻辑结构有哪几种?用程序框图分别如何表示?步骤n步骤n+1顺序结构条件结构满足条件?步骤A步骤B是否(1)满足条件?步骤A是否(2)循环结构循环体满足条件?是否直到型循环体满足条件?是否当型123、任何一个程序框图必定包含顺序结构;、条件结构最显著的特征是含有判断框;、循环结构一定包含条件结构;4、循环结构包含两个要素:循环体:两个或两个以上的处理框,控制器:判断框(决定什么时候终止).5、循环体中最显著的变量是“计数变量”计数变量的作用一定要①、②、搞清楚.注意:2.在学习上,我们要求对实际问题能用自然语言设计一个算法,再根据算法的逻辑结构画出程序框图,同时,还要能够正确阅读、理解程序框图所描述的算法的含义,这需要我们对程序框图的画法有进一步的理解和认识.例1:已知函数右面流程图表示的是给定x值,求其相应函数值的算法,请将流程图补充完整,其中①处应填②处应填()|3|fxx3x开始结束①y输出x输入3yx②否是3xy思考3:你能画出求分段函数2,131,011,0xxyxxxxìï+>ïïïï=-££íïïï-<ïïî的值的程序框图吗?思考3:你能画出求分段函数的值的程序框图吗?开始输入xx>1?输出y结束x≥0?否是y=x+2是y=3x-1否y=1-x0,110,131,2xxxxxxy知识探究(一):多重条件结构的程序框图思考1:解关于x的方程ax+b=0的算法步骤如何设计?第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;否则,输出“方程无实数解”.第一步,输入实数a,b.第二步,判断a是否为0.若是,执行第三步;否则,计算,并输出x,结束算法.bxa=-思考2:该算法的程序框图如何表示?开始输入a,ba=0?是b=0?输出x结束输出“方程的解为任意实数”是输出“方程无实数根”否否bxa=-例1设计一个求解一元二次方程ax2+bx+c=0的算法,并画出程序框图表示.理论迁移算法分析:第一步,输入三个系数a,b,c.第二步,计算△=b2-4ac.第三步,判断△≥0是否成立.若是,则计算;否则,输出“方程没有实数根”,结束算法.,22bpqaa=-=V第四步,判断△=0是否成立.若是,则输出x1=x2=p,否则,计算x1=p+q,x2=p-q,并输出x1,x2.程序框图:开始输入a,b,c△=b2-4ac≥△0?△=0?否x1=p+q输出x1,x2结束否是2bpa=-x2=p-q输出x1=x2=p是输出“方程没有实数根”aq2例2某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.第三步,判断所得的结果是否大于300.若是,则输出该年的年份;否则,返回第二步.第一步,输入2005年的年生产总值.第二步,计算下一年的年生产总值.算法分析:(3)控制条件:当“a>300”时终止循环.(1)循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则t=0.05a,a=a+t,n=n+1.(2)初始值:n=2005,a=200.循环结构:开始n=2005a=200t=0.05aa=a+tn=n+1a>300?结束输出n是否程序框图:思考1:用“二分法”求方程的近似解的算法如何设计?220(0)xx知识探究(二):混合逻辑结构的程序框图第一步,令f(x)=x2-2,给定精确度d.第二步,确定区间[a,b],满足f(a)·f(b)<0.第三步,取区间中点.2abm第四步,若f(a)·f(m)<0,则含零点的区间为[a,m];否则,含零点的区间为[m,b].将新得到的含零点的区间仍记为[a,b].第五步,判断[a,b]的长度是否小于d或f(m)是否等于0.若是,则m是方程的近似解;否则,返回第三步.思考2:该算法中哪几个步骤可以用顺序结构来表示?这个顺序结构的程序框图如何?f(x)=x2-2输入精确度d和初始值a,b2abm思考3:该算法中第四步是什么逻辑结构?这个步骤用程序框图如何表示?f(a)f(m)<0?a=mb=m是否思考4:该算法中哪几个步骤构成循环结构?这个循环结构用程序框图如何表示?第三步第四步|a-b|