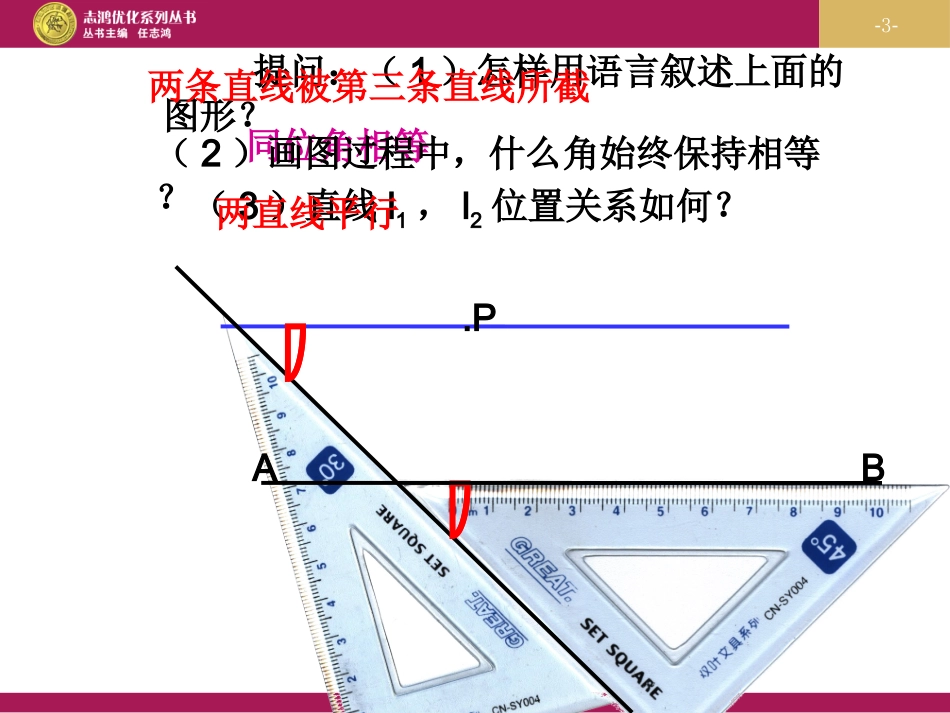
55.2.2平行线的判定1济水一中赵小凤-2-3.过点P作直线AB的平行线。1.平行线的定义:在同一平面内,两条直线不相交,就叫平行线.2.如果直线a//b,b//c,那么a与c什么关系?为什么?如果两条直线都与第三条直线平行,那么这两条直线也互相平行。-3-提问:(1)怎样用语言叙述上面的图形?两条直线被第三条直线所截同位角相等(2)画图过程中,什么角始终保持相等?(3)直线l1,l2位置关系如何?两直线平行AB.P-4-两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行平行线判定方法1:几何语言表述:∵∠1=2∠(已知)∴ABCD∥(同位角相等,两直线平行)-5-已知∠1=120°,∠2=60°,试说明AB//CD.解:理由如下,∵∠CEF=180°-_____,∠2=60°,∴∠CEF=180°-____=_______。∵∠1=120°,∴_______=________()。∴AB//CD(_______相等,两直线_______)∠2∠CEF∠1同位角平行60°120°等量代换-6-探究:内错角∠3与∠4满足什么关系时ABCD∥呢?为什么?EDAB132C4F∵∠3=4∠,∠1=4(∠对顶角相等),∴∠1=3∠(等量代换)。∴ABCD∥。当∠3=4∠时,AB//CD-7-EDAB132C4F两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.∵∠3=4∠(已知)∴ABCD∥(内错角相等,两直线平行)-8-探究:同旁内角∠4与∠2在数量上满足什么关系时,两直线平行?EDAB132C4F∵∠2+4=180°∠,∠2+3=180°∠,∴∠3=4∠(同角的补角相等)∴ABCD∥。(内错角相等,两直线平行)能不能根据同位角相等,两直线平行来证-9-EDAB132C4F两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.∵∠2+4=180∠°(已知),∴ABCD∥。(同旁内角互补,两直线平行)-10-例:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?平行,理由:如图,∵ba,ca⊥⊥(已知),∴∠1=2=90°∠(垂直定义)。∴bc∥(同位角相等,两直线平行)。abc12-11-总结判定两条直线平行的方法:1.平行线的定义:2.若ab∥,bc∥,则ac∥。(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)3.同位角相等内错角相等同旁内角互补两直线平行-12-1.如图所示,在下列条件中,不能判断∥的是().A.∠1=3∠B.∠2=3∠C.∠4+5=180°∠D.∠2+4=180°∠FEABCD1232.如图,回答下列问题,并说明理由.(1)由∠D=1,∠可判定哪两条直线平行?(2)由∠2=3,∠可判定哪两条直线平行?(3)由此你还能得出哪两条直线平行?为什么?1L2L1L2L