二次函数的图象和性质VIP免费

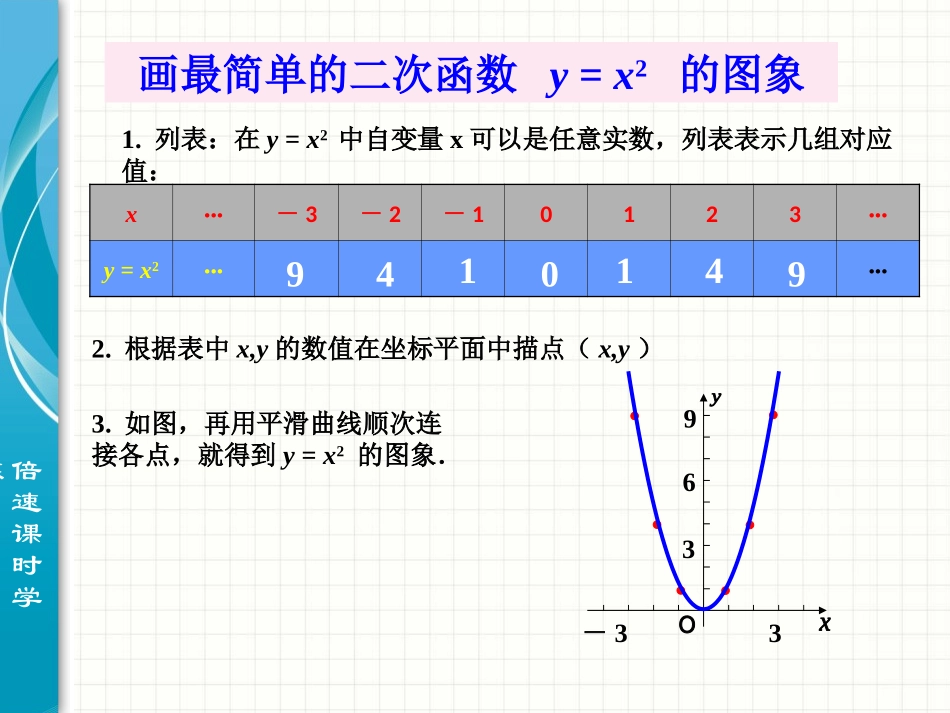
二次函数的图象和性质二次函数y=ax的图象和性质倍速课时学练(1)一次函数的图象是一条_____(2)通常怎样画一个函数的图象？直线(3)二次函数的图象是什么形状呢？列表、描点、连线结合图象讨论性质是数形结合的研究函数的重要方法．我们得从最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质．倍速课时学练1.列表：在y=x2中自变量x可以是任意实数，列表表示几组对应值：x···－3－2－10123···y=x2······2.根据表中x,y的数值在坐标平面中描点（x,y）画最简单的二次函数y=x2的图象－3336901491493.如图，再用平滑曲线顺次连接各点，就得到y=x2的图象．倍速课时学练二次函数y=x2的图象是一条曲线，它的形状类似于投篮球时球在空中所经过的路线，只是这条曲线开口向上，这条曲线叫做抛物线y=x2，y轴是抛物线y=x2的对称轴，抛物线y=x2与它的对称轴的交点（0，0）叫做抛物线y=x2的顶点，它是抛物线y=x2的最低点．－33369二次函数的图象都是抛物线，它们的开口或者向上或者向下．一般地，二次函数y=ax2+bx+c（a≠0）的图象叫做抛物线y=ax2+bx+c实际上，每条抛物线都有对称轴，抛物线与对称轴的交点叫做抛物线的顶点．顶点是抛物线的最低点或最高点．倍速课时学练例1在同一直角坐标系中，画出函数的图象．222,21xyxy解：分别填表，再画出它们的图象，如图x···－4－3－2－101234·········x···－2－1.5－1－0.500.511.52·········212yx22yx84.520.5084.520.584.520.5084.520.5－222464－48212yx22yx2yx倍速课时学练函数的图象与函数y=x2的图象相比，有什么共同点和不同点？222,21xyxy－222464－48212yx22yx2yx相同点：开口都向上，顶点是原点而且是抛物线的最低点，对称轴是y轴不同点：a要越大，抛物线的开口越小．倍速课时学练你画出的图象与图中相同吗？探究画出函数的图象，并考虑这些抛物线有什么共同点和不同点．2222,21,xyxyxy倍速课时学练x···－4－3－2－101234·········x···－2－1.5－1－0.500.511.52·········212yx22yx－8－4.5－2－0.50－8－4.5－2－0.5－8－4.5－2－0.50－8－4.5－2－0.5－22－2－4－64－4－8212yx22yx2yx对比抛物线，y=x2和y=－x2.它们关于x轴对称吗？一般地，抛物线y=ax2和y=－ax2呢？倍速课时学练一般地，抛物线y=ax2的对称轴是y轴，顶点是原点．当a>0时，抛物线的开口向上，顶点是抛物线的最低点，a越大，抛物线的开口越小；当a<0时，抛物线的开口向_______,顶点是抛物线的最________点，a越大，抛物线的开口越_________．下高大倍速课时学练函数a的符号图象开口方向对称轴顶点坐标有最高或最低点最值y＝ax2a>0向上y轴(0,0)最低点当x＝0时，ymin＝0a<0向下最高点当x＝0时，ymax＝0归纳：(3)当a>0时，a越大，抛物线的开口越______；当a<0时，a越大，抛物线的开口越______．小大倍速课时学练(1)求函数满足条件的n的值；(2)当n为何值时，抛物线有最高点；(3)当n为何值时，抛物线开口向上．思路点拨：(1)n需满足两个条件：①n2＋n－4＝2；②n＋2≠0.(2)(3)中n值的确定都与二次项系数的正负有关．【例3】已知y＝(n＋2)24nnx是关于x的二次函数．【跟踪训练】倍速课时学练解得n1＝2，n2＝－3.即当n＝2或n＝－3时，原函数为二次函数．(2)当n＝－3时，n＋2<0，∴当n＝－3时，抛物线有最高点．(3)当n＝2时，n＋2>0，∴n＝2时，抛物线开口向上．解：(1)由题意，得n2＋n－4＝2，n＋2≠0，倍速课时学练【跟踪训练】2．已知a<－1，点(a－1，y1)，(a，y2)，(a＋1，y3)都在函)数y＝x2的图象上，则(A．y1b>d>c