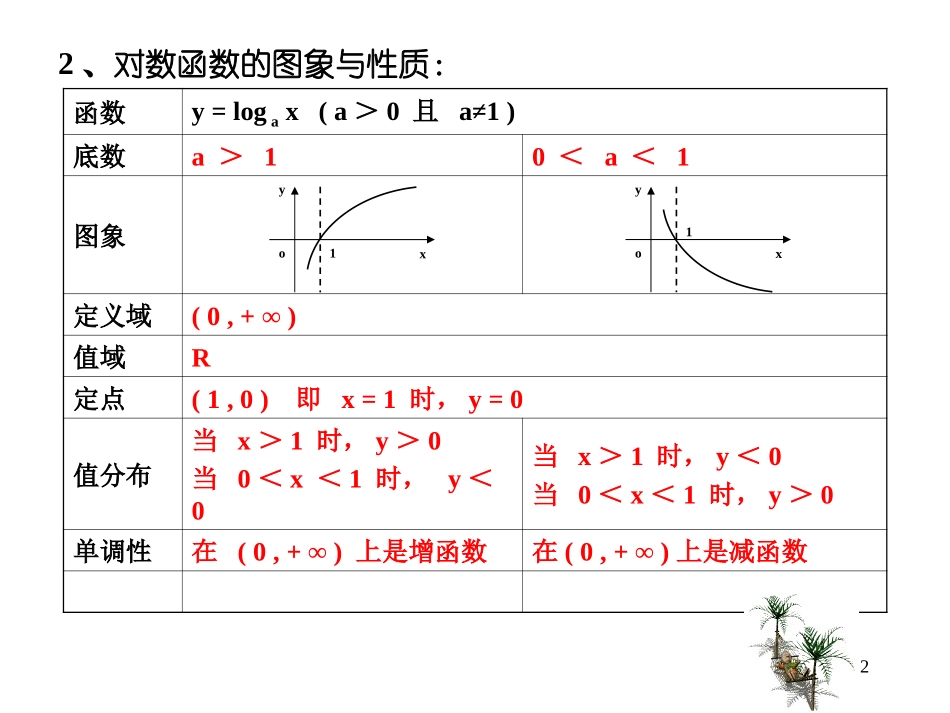
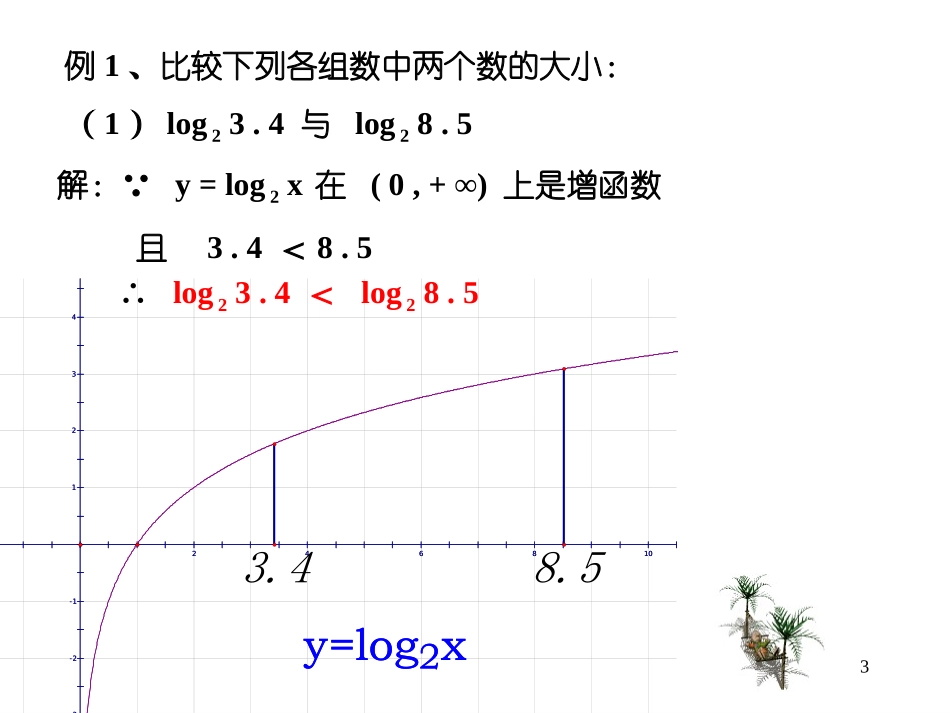
对数函数(2)22、对数函数的图象与性质:函数y=logax(a>0且a≠1)底数a>10<a<1图象定义域(0,+∞)值域R定点(1,0)即x=1时,y=0值分布当x>1时,y>0当0<x<1时,y<0当x>1时,y<0当0<x<1时,y>0单调性在(0,+∞)上是增函数在(0,+∞)上是减函数1xyo1xyo34321-1-2-3246810y=log2x4321-1-2-3246810y=log2x3.48.5例1、比较下列各组数中两个数的大小:(1)log23.4与log28.5解:∵y=log2x在(0,+∞)上是增函数且3.4<8.5∴log23.4<log28.54例1、比较下列各组数中两个数的大小:(2)log0.31.8与log0.32.7解:∵y=log0.3x在(0,+∞)上是减函数且1.8<2.7∴log0.31.8>log0.32.71.41.210.80.60.40.2-0.2-0.4-0.6-0.8-1-1.2-1.4-0.50.511.522.533.5y=log0.3x1.41.210.80.60.40.2-0.2-0.4-0.6-0.8-1-1.2-1.4-0.50.511.522.533.5y=log0.3x1.82.752.521.510.5-0.5-1-1.51234567y=logax2.521.510.5-0.5-1-1.51234567y=logax5.15.9例1、比较下列各组数中两个数的大小:(3)loga5.1与loga5.9(0<a<1)解:∵y=logax(0<a<1)在(0,+∞)上是减函数且5.1<5.9∴loga5.1>loga5.9小结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1(a>1时为增函数0