第8章 相量法修改VIP免费

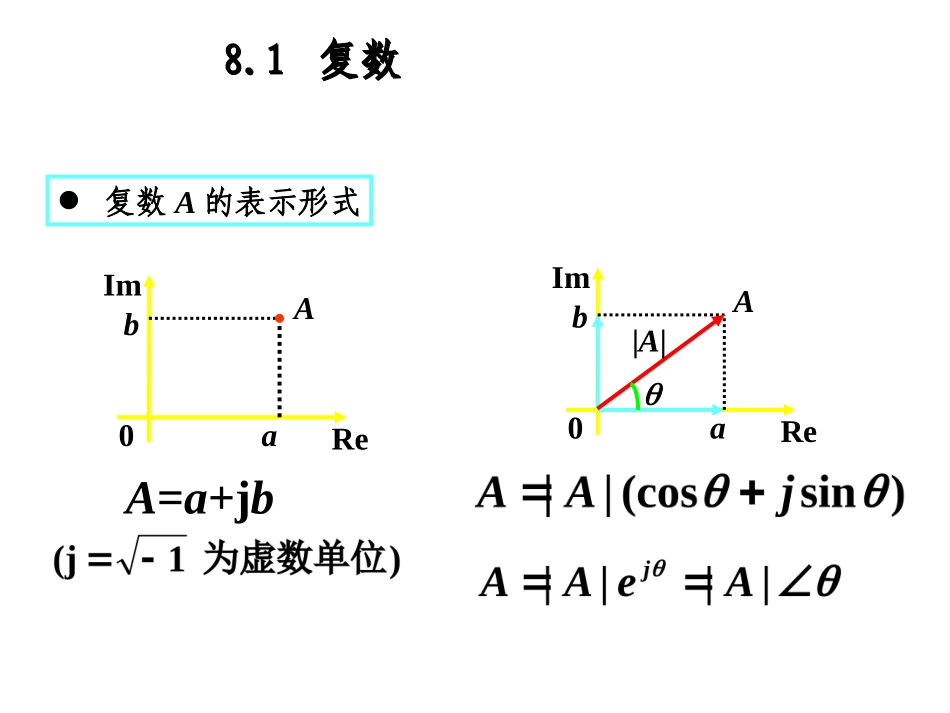
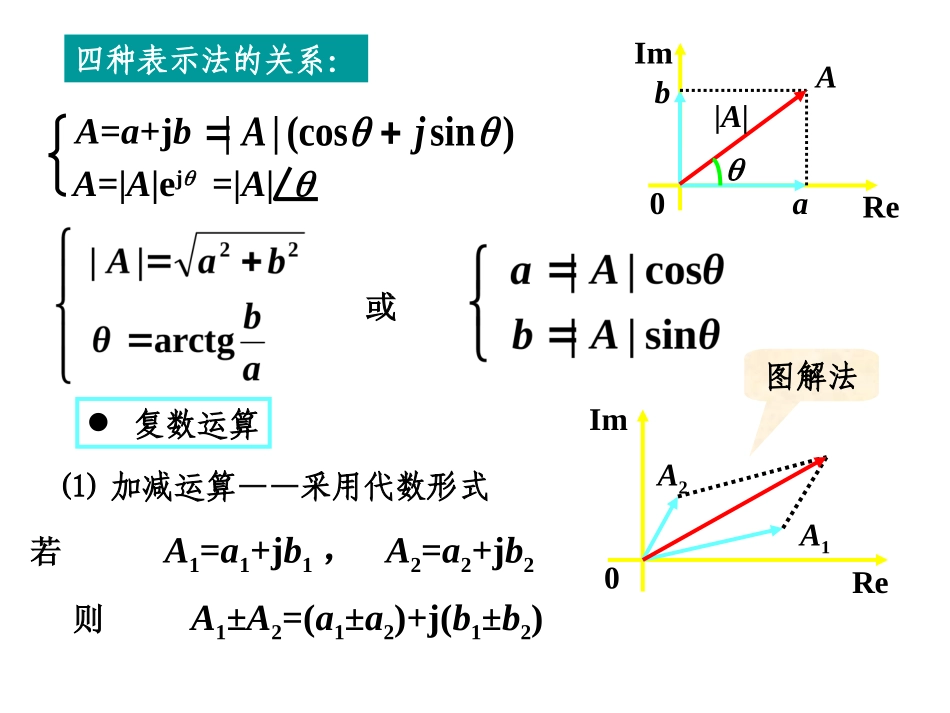
第8章相量法第8章相量法2.正弦量的相量表示3.电路定理的相量形式；重点：1.正弦量的表示、相位差；复数A的表示形式AbReIma0A=a+jbAbReIma0|A|8.1复数8.1复数四种表示法的关系：或复数运算则A1±A2=(a1±a2)+j(b1±b2)(1)加减运算——采用代数形式若A1=a1+jb1，A2=a2+jb2A1A2ReIm0AbReIma0|A|图解法A=a+jbA=|A|ej=|A|)sin(cos||jA(2)乘除运算——采用极坐标或指数形式若A1=|A1|1，A2=|A2|2除法：模相除，角相减。乘法：模相乘，角相加。则:(3)旋转因子：复数ej=cos+jsin=1∠A•ej相当于A逆时针旋转一个角度，而模不变。故把ej称为旋转因子。AReIm0A•ej故+j,–j,-1都可以看成旋转因子。几种不同值时的旋转因子ReIm0正弦电流电路激励和响应均为正弦量的电路称为正弦电路或交流电路。8-2正弦量1.正弦量瞬时值表达式：i(t)=Imcos(t+)波形：tiO/T周期T(period)和频率f(frequency):频率f：每秒重复变化的次数。周期T：重复变化一次所需的时间。单位：Hz，赫(兹)单位：s，秒Tf1(1)幅值(amplitude)(振幅、最大值)Im(2)角频率(angularfrequency)2.正弦量的三要素(3)初相位(initialphaseangle)tiO/TIm2t单位：rad/s，弧度/秒反映正弦量变化幅度的大小。相位变化的速度，反映正弦量变化快慢。反映正弦量的计时起点。i(t)=Imcos(t+)同一个正弦量，计时起点不同，初相位不同。tiO一般规定：||。=0=±=－/2对任一正弦量，初相是允许任意指定的，但对于同一电路系统中的许多相关的正弦量，只能相对于共同的计时零点确定各自的相位。3.同频率正弦量的相位差(phasedifference)。设u(t)=Umcos(t+u),i(t)=Imcos(t+i)则相位差：=(t+u)-(t+i)=u-i>0，u超前i角，或i落后u角(u比i先到达最大值)；<0，i超前u角，或u滞后i角,i比u先到达最大值。等于初相位之差规定：||(180°)。tu,iuiuiO＝0，同相：=(180o)，反相：特殊相位关系：tu,iui0tu,iui0=＝u领先i,不说u落后i3/2；i落后u,不说i领先u3/2。tu,iui0同样可比较两个电压或两个电流的相位差。例计算下列两正弦量的相位差。解不能比较相位差两个正弦量进行相位比较时应满足同频率、同函数、同符号，且在主值范围比较。4.周期性电流、电压的有效值周期性电流、电压的瞬时值随时间而变，为了衡量其大小工程上采用有效值来表示。周期电流、电压有效值(effectivevalue)定义R直流IR交流i电流有效值定义为TttiTI02defd)(1TttiTI02defd)(1有效值也称均方根值(root-meen-square)物理意义同样，可定义电压有效值：TttuTU02defd)(1TttuTU02defd)(1正弦电流、电压的有效值II2mmII707.0或（1）工程上说的正弦电压、电流一般指有效值，如设备铭牌额定值、电网的电压等。但绝缘水平、耐压值指的是最大值。因此，在考虑电器设备的耐压水平时应按最大值考虑。（2）测量中，交流电压、电流表读数一般为有效值。（3）区分电压、电流的瞬时值、最大值、有效值的符号。注UUuIIi,,,,,mm8-3相量法的基础Ri(t)u(s)L+-C问题：当u(s)为正弦量时，电路中的电压和电流的频率会变化吗？因此，线性非时变电路在正弦电源激励下，各支路电压、电流的特解都是与激励同频率的正弦量，当电路中存在多个同频率的正弦量时该结论也成立。正弦量乘以常数，正弦量的微积分，同频正弦量的代数和等运算，其结果仍为一个同频率的正弦量。正弦量复数变换的思想所以，只要确定初相位和有效值(或最大值)就行了。造一个复函数)j(2)(ΨtIetF对F(t)取实部)()cos(2)](Re[tiΨtItF任意一个正弦时间函数都有唯一与其对应的复数函数。)j(2)()cos(2ΨtIetFΨtIi)sin(2j)cos(2ΨtIΨtI无物理意义是一个正弦量有物理意义正弦量的相量表示下页上页结论返回F(t)包含了三要素：I、、＝＝＝＝＝＝＝＝＝＝＝＝,＝F(t)还可以写成tteIeIetFjj22)(j＝＝＝下页上...