第02章 算法与数据结构-04树和二叉树1VIP免费

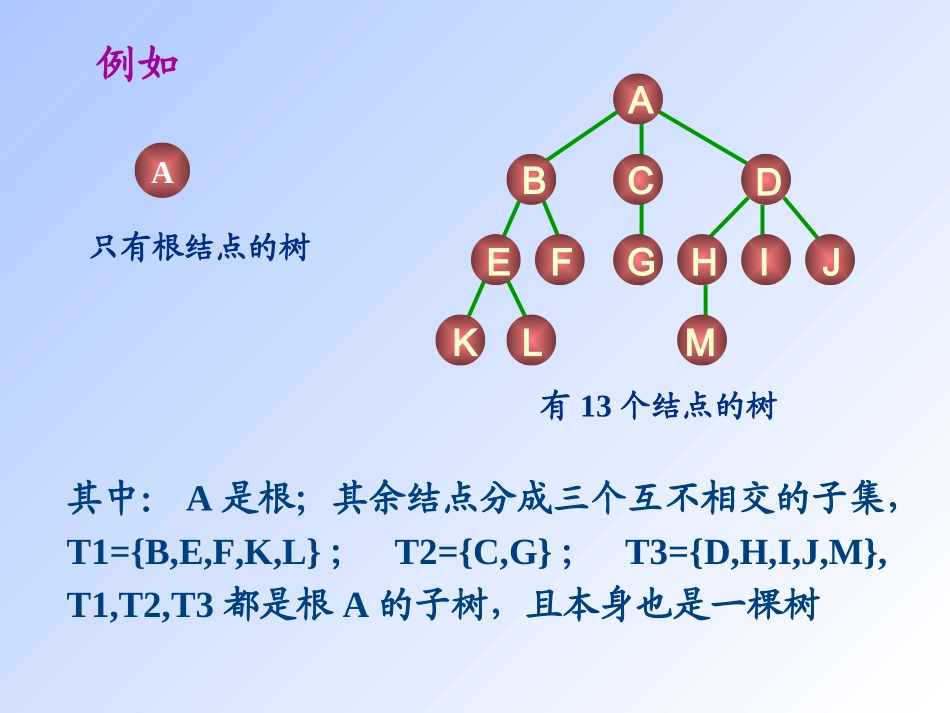
第6章树和二叉树树的概念和基本术语二叉树二叉树遍历二叉树的计数树与森林霍夫曼树树的概念和基本术语树的定义树是由n(n0)个结点的有限集合。如果n=0，称为空树；如果n>0，则有且仅有一个特定的称之为根(Root)的结点，它只有直接后继，但没有直接前驱；当n>1，除根以外的其它结点划分为m(m>0)个互不相交的有限集T1,T2,…,Tm，其中每个集合本身又是一棵树，并且称为根的子树(SubTree)。。ACGBDEFKLHMIJ例如A只有根结点的树有13个结点的树其中：A是根；其余结点分成三个互不相交的子集，T1={B,E,F,K,L}；T2={C,G}；T3={D,H,I,J,M},T1,T2,T3都是根A的子树，且本身也是一棵树树的基本术语1层2层4层3层height=4ACGBDEFKLHMIJ结点结点结点的度结点的度叶结点叶结点分支结点分支结点子女子女双亲双亲兄弟兄弟祖先祖先子孙子孙结点层次结点层次树的深树的深度度树的度树的度森林森林二叉树(BinaryTree)定义五种形态一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。LLRR特点每个结点至多只有两棵子树（二叉树中不存在度大于2的结点）性质1在二叉树的第i层上至多有2i－1个结点。(i1)[证明用归纳法]证明：当i=1时，只有根结点，2i-1=20=1。假设对所有j，i>j1，命题成立，即第j层上至多有2j-1个结点。由归纳假设第i-1层上至多有2i－2个结点。由于二叉树的每个结点的度至多为2，故在第i层上的最大结点数为第i-1层上的最大结点数的2倍，即2*2i－2=2i-1。性质性质2深度为k的二叉树至多有2k-1个结点(k1)。证明：由性质1可见，深度为k的二叉树的最大结点数为kii112＝20+21+…+2k-1=2k-1kii1(层上的最大结点数）第＝性质3对任何一棵二叉树T,如果其叶结点数为n0,度为2的结点数为n2,则n0＝n2＋1.证明：若度为1的结点有n1个，总结点个数为n，总边数为e，则根据二叉树的定义，n=n0+n1+n2e=2n2+n1=n-1因此，有2n2+n1=n0+n1+n2-1n2=n0-1n0=n2+1定义1满二叉树(FullBinaryTree)一棵深度为k且有2k-1个结点的二叉树称为满二叉树。两种特殊形态的二叉树621754389101113141512满二叉树2154367216543非完全二叉树定义2完全二叉树(CompleteBinaryTree)若设二叉树的高度为h，则共有h层。除第h层外，其它各层(0h-1)的结点数都达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。621754389101112完全二叉树性质4具有n(n0)个结点的完全二叉树的深度为log2(n)＋1证明：设完全二叉树的深度为h，则根据性质2和完全二叉树的定义有2h－1-10,则i的双亲为(i-1)/2若2*i+1leftChild);destroy(current->rightChild);deletecurrent;}}基本算法B...