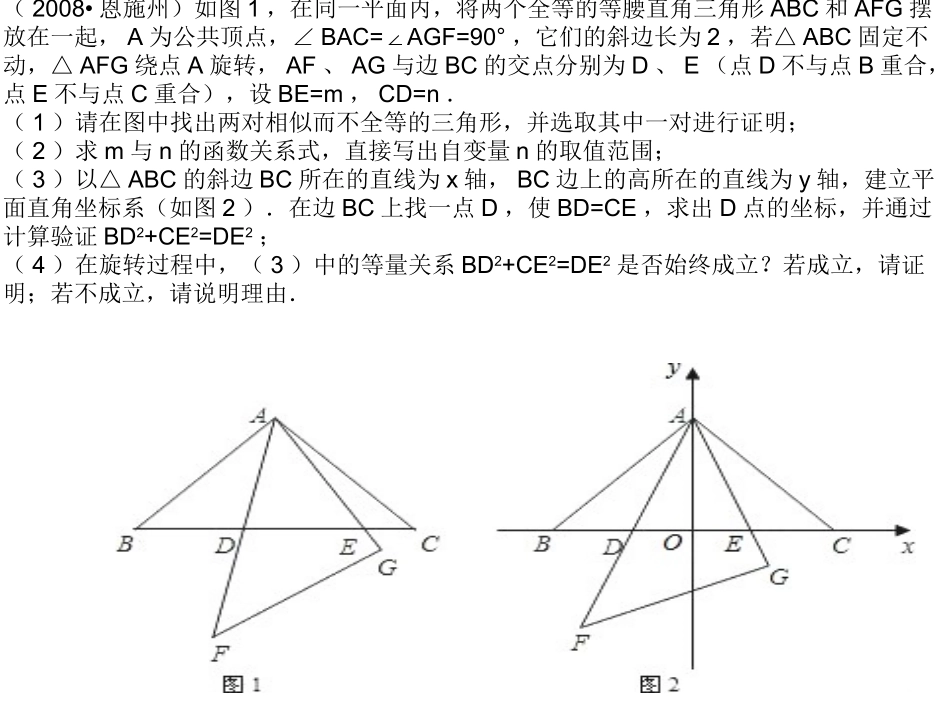
(2008•恩施州)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=AGF=90°∠,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明;(2)求m与n的函数关系式,直接写出自变量n的取值范围;(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2;(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立?若成立,请证明;若不成立,请说明理由.如图3,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上,试问这样截下的矩形铁皮周长能否等于8dm?如图4,在一直角三角形中建造一个内接于△ABC的矩形水池DEFN.其中DE在AB上,AC=8,BC=6.(1)求△ABC中AB边上的高h;(2)设DN=x,当x取何值时,水池DEFN的面积最大?(3)实际施工时,发现在AB上距B点1.85处有一棵大树,问这棵大树是否位于最大矩形水池的边上?.如图,O⊙1、⊙O2交于A、B两点,点O1在⊙O2上,两圆的连心线交⊙O1于E、D,交⊙O2于F,交AB于C,请根据图中所给的已知条件(不再标注其他字母,不再添加任何辅助线),写出两个线段之间的关系式.O2O1FECDBA如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D。(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;(2)当AP的长为何值时,S△PCQ=S△ABC1在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动,回答下列问题:(1)运动开始后第几秒时,△PBQ的面积等于8cm2(2)设运动开始后第t秒时,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量t的取值范围;t为何值时S最小?求出S的最小值。CDQBPA